Creating curious conversations: Using a wise intervention to improve political discourse

Online Supplement

Authors
Affiliations

Patrick E. McKnight

George Mason University

Todd B. Kashdan

George Mason University

Kerry Kelso

Logan Craig

Madeleine Gross

University of California, Santa Barbara

INTRODUCTION

This document is an online supplement for the publication “Creating curious conversations: Using a wise intervention to improve political discourse” in Nature: Scientific Reports. Below, we provide specific details about the data, measures, and analyses used in the paper. We also provide the code used to generate the tables and figures in the paper. The code is provided along with a list of libraries. Finally, we provide the runtime details of the analyses and results at the end for later verification and integrity checking. Thank you for your interest in our work.

Code 
# load libs
library(haven)
library(ggplot2)
library(dplyr)
library(tidyr)
library(modelsummary)
library(broom)
library(kableExtra)
library(gt)
library(knitr)
library(emmeans)
library(sjlabelled)
library(lavaan)
library(lavaanPlot)
library(psych)
library(semPlot)
library(semTools)
library(summarytools)
library(devtools)
#devtools::install_github("Aaron0696/aaRon")
library(aaRon)
aaRon::use.style(mode = "work")
Code 
library(sjPlot)
library(lme4)
library(lmerTest)
library(forcats)

# functions used below
getQuests <- function(x) {
  as.data.frame(unlist(as.list(sjlabelled::get_label(x))))  
}

OrigDatWithScored5DCR <- function(data, subset) {
  tmp <- data[, subset]
  names(tmp) <- c("id","JE1", "JE2", "JE3", "JE4", "DS1", "DS2", "DS3", "DS4", 
                 "ST1", "ST2", "ST3", "ST4", "TS1", "TS2", "TS3", "TS4", 
                 "GSC1", "GSC2", "GSC3", "GSC4")
  
  # Convert all scale items to numeric (excluding id)
  tmp[, -1] <- lapply(tmp[, -1], as.numeric)
  
  # Correctly calculate means (excluding id column)
  tmp$JE <- rowMeans(tmp[, 2:5], na.rm = TRUE)
  tmp$DS <- rowMeans(tmp[, 6:9], na.rm = TRUE)
  tmp$ST <- rowMeans(tmp[, 10:13], na.rm = TRUE)
  tmp$TS <- rowMeans(tmp[, 14:17], na.rm = TRUE)
  tmp$GSC <- rowMeans(tmp[, 18:21], na.rm = TRUE)
  
  return(tmp)
}


# OrigDatWithScored5DCR <- function(data, subset) {
#   tmp <- data[, subset]
#   names(tmp) <- c("id","JE1", "JE2", "JE3", "JE4", "DS1", "DS2", "DS3", "DS4", "ST1", "ST2", "ST3", "ST4", "TS1", "TS2", "TS3", "TS4", "GSC1", "GSC2", "GSC3", "GSC4")
#   tmp$JE <- rowMeans(tmp[, 1:4])
#   tmp$DS <- rowMeans(tmp[, 5:8])
#   tmp$ST <- rowMeans(tmp[, 9:12])
#   tmp$TS <- rowMeans(tmp[, 13:16])
#   tmp$GSC <- rowMeans(tmp[, 17:20])
#   return(tmp)
# }

DATA SOURCES

We used three studies that were preregistered and available upon request for the current paper.

Study 1: Poor Mans Nat Rep Sample: Poor Mans Nat Rep Sample Oct 2021_November 12, 2021_11.15 orig.sav

Study 2: High Powered, Pre-Registered Test: OD Intervention Preregistered Test Oct 2021 orig.sav

Study 3: (a) Pre-intervention measures: Streamlined Intervention PreMeasures For Real_February 6, 2022_12.29 (b) Intervention: Streamlined OD Intervention Jan 2022_February 6, 2022_12.40

The original raw data files came in the form of SPSS .sav files. The data were collected in Qualtrics and then exported to SPSS. We read in the data and then evaluated the integrity and computed necessary variables. Each of those steps is outlined below. Selected data for the paper are available upon request as three separate files. We omitted other variables - beyond those included in these analyses - because we intend to publish that material in subsequent papers.

Code 
# Data Sources
dat <- read_sav("./Data_Final/Poor Mans Nat Rep Sample Oct 2021_November 12, 2021_11.15 orig.sav")
dat2 <- read_sav("./Data_Final/OD Intervention Preregistered Test Oct 2021 orig.sav")
dat3a <- read_sav("./Data_Final/Streamlined Intervention PreMeasures For Real_February 6, 2022_12.29.sav")
dat3b <- read_sav("./Data_Final/Streamlined OD Intervention Jan 2022_February 6, 2022_12.40.sav")
dat3 <- merge(dat3a, dat3b, by = "PROLIFIC_PID")

## Create ID variable for all data - not mergeable between studies
dat$id <- c(1:nrow(dat)) # no id in the original data, yep, none
dat2$id <- c(1:nrow(dat2))
dat3a$id <- c(1:nrow(dat3a))
dat3b$id <- c(1:nrow(dat3b))
dat3$id <- c(1:nrow(dat3))

# create a quick data summary for each data frame
dfSUM <- data.frame(Study1 = dim(dat), Study2 = dim(dat2), Study3 = dim(dat3))
rownames(dfSUM) <- c("Sample Size:", "Number of Variables:")
kable(dfSUM)
Study1 Study2 Study3
Sample Size: 1465 466 651
Number of Variables: 148 299 290

Demographics and Descriptives

Code 
# Create the data frame with demographic information
demographic_data <- data.frame(
  Category = c(
    "Gender", "", "", "",
    "Race", "", "", "", "", "", "","",
    "Age (M (SD))"
  ),
  Subcategory = c(
    "%Male", "% Female", "% Non-binary", "",
    "%White", "%Black", "%Hispanic", "%Asian/Pacific Islander", 
    "%Arab/Middle Eastern", "%Mixed", "%Other","",
    ""
  ),
#  Study_1 = c(
#    "48.5", "50.1", "1.4", "",
#    "70.4", "11.1", "6.4", "10.3", 
#    "-", "-", "1.8",
#    "36.53, 12.72"
#  ),
  Study_1 = c(
    "44.0", "55.2", "0.7", "",
    "72.8", "10.3", "10.9", "3.5", 
    "0.1", "-", "2.5","",
    "47.51 (18.80)"
  ),
  Study_2 = c(
    "20.1", "77.9", "2.0", "",
    "77.1", "5.0", "7.0", "7.8", 
    "0.3", "-", "2.8","",
    "31.55 (12.94)"
  ),
  Study_3 = c(
    "28.0", "71.4", "0.6", "",
    "77.5", "4.3", "5.3", "9.8", 
    "0.8", "-", "2.3","",
    "38.04 (14.46)"
  ),
  stringsAsFactors = FALSE
)

# Create the kableExtra table
demographic_table <- demographic_data %>%
  kbl(caption = "Demographic breakdown for every study in the manuscript",
      booktabs = TRUE) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed"), 
                full_width = FALSE,
                position = "center") %>%
  column_spec(1, bold = ifelse(demographic_data$Category != "", TRUE, FALSE)) %>%
  collapse_rows(columns = 1, valign = "top") %>%
  row_spec(0, bold = TRUE)

# Display the table
demographic_table
Demographic breakdown for every study in the manuscript
Category Subcategory Study_1 Study_2 Study_3
Gender %Male 44.0 20.1 28.0
% Female 55.2 77.9 71.4
% Non-binary 0.7 2.0 0.6
Race %White 72.8 77.1 77.5
%Black 10.3 5.0 4.3
%Hispanic 10.9 7.0 5.3
%Asian/Pacific Islander 3.5 7.8 9.8
%Arab/Middle Eastern 0.1 0.3 0.8
%Mixed - - -
%Other 2.5 2.8 2.3
Age (M (SD)) 47.51 (18.80) 31.55 (12.94) 38.04 (14.46)

Data Management

We used the original data files exported from the Qualtrics surveys; all variable names appear as they were observed in these original sources. The haven package in R helped us read and convert SPSS sav files into native R binary objects. Some of the key variables and their actual wording are detailed below.

Recode pol_b to binary variable

We recoded the variable pol_b and pol_party_b to binary variables since we needed at least one variable (for each) that we could determine political ideology and party affiliation. Our other variable “pol_mod_b” contained too many missing values due to skip patterns that this variable was our hope to restore some classification to the data. The pol_b question simply asked respondents to reply with how they viewed their political ideology from “extremely liberal” = 1 to “extremely conservative” = 7 with a middle category “moderate/middle of the road” = 4. We split the variable at 4 indicating only those who endorsed being conservative as conservative; thus, 4 or less indicated liberal and higher than 4 indicated conservative. The final variables are labeled conservative_bin and republican_b. We also created a factor variables for each for easier interpretation later should we use political ideology or party as predictors in our models.

Code 
#kable(table(dat$conservative_f))

# Conservative Recoded
dat$conservative <- dat$pol_b
dat$conservative_bin <- ifelse(dat$pol_b > 4, 2, 1)
dat$conservative_bin <- ifelse(dat$pol_b == 4, dat$pol_mod_b, dat$conservative_bin)
dat$conservative_bin <- dat$conservative_bin - 1 # key to make it 0,1

# Republican Recoded
dat$republican_b <- ifelse(dat$pol_party_b > 4, 2, 1)
dat$republican_b <- ifelse(dat$pol_party_b == 4, dat$pol_inde_b, dat$republican_b)
dat$republican_b <- dat$republican_b - 1 # key to make it 0,1

# convert conservative_bin and republican_b to factors with labels
dat$conservative_f <- factor(dat$conservative_bin, levels = c(0, 1), labels = c("Liberal", "Conservative"))
dat$republican_f <- factor(dat$republican_b, levels = c(0, 1), labels = c("Democrat", "Republican"))



# Conservative Factor alone
dat %>% 
  select(conservative_f) %>%
  table() %>%
  kable()
conservative_f Freq
Liberal 632
Conservative 704
Code 
# Republican Recoded
dat$republican_b <- ifelse(dat$pol_party_b > 4, 2, 1)
dat$republican_b <- ifelse(dat$pol_party_b == 4, dat$pol_inde_b, dat$republican_b)
dat$republican_b <- dat$republican_b - 1 # key to make it 0,1

#table(dat$republican_b)

#table(dat$conservative_bin, dat$republican_b)

# convert conservative_bin and republican_b to factors with labels
dat$conservative_f <- factor(dat$conservative_bin, levels = c(0, 1), labels = c("Liberal", "Conservative"))
dat$republican_f <- factor(dat$republican_b, levels = c(0, 1), labels = c("Democrat", "Republican"))

kable(table(dat$conservative_f, dat$republican_f))
Democrat Republican
Liberal 531 98
Conservative 169 531
Code 
# compute marginal means and percentages for the table above

# dat %>%
#   group_by(conservative_f, republican_f) %>%
#   summarise(n = n()) %>%
#   mutate(percentage = n / sum(n) * 100) %>%
#   kable()
Code 
# Create a new dataframe instead of modifying the original
dat_recoded <- dat %>% 
  mutate(
    # Store original political orientation value
    conservative = pol_b,
    
    # Initial binary coding: values > 4 become 2, others become 1
    conservative_bin = if_else(pol_b > 4, 2, 1),
    
    # Special handling for middle value (4): 
    # Use the pol_mod_b value for these cases to restore classification
    conservative_bin = if_else(pol_b == 4, pol_mod_b, conservative_bin),
    
    # Convert to 0-1 scale instead of 1-2
    conservative_bin = conservative_bin - 1,
    
    # Create factor version for use as predictor in models
    conservative_factor = factor(conservative_bin, 
                                levels = c(0, 1),
                                labels = c("Liberal", "Conservative"))
  )

# Create ideology labels for the table
ideology_labels <- c(
  "1" = "Extremely Liberal (1)",
  "2" = "Liberal (2)",
  "3" = "Slightly Liberal (3)",
  "4" = "Moderate (4)",
  "5" = "Slightly Conservative (5)",
  "6" = "Conservative (6)",
  "7" = "Extremely Conservative (7)"
)

# Build the table with counts and percentages
ideology_table <- dat_recoded %>% 
  count(conservative_bin, pol_b) %>%
  group_by(pol_b) %>%
  mutate(percentage = sprintf("%.1f%%", 100 * n / sum(n))) %>%
  ungroup() %>%
  mutate(
    classification = if_else(conservative_bin == 1, "Conservative", "Liberal"),
    value_label = ideology_labels[as.character(pol_b)],
    display_value = paste0(n, " (", percentage, ")")
  ) %>%
  select(classification, pol_b, value_label, display_value) %>%
  pivot_wider(
    names_from = classification,
    values_from = display_value,
    values_fill = "0 (0.0%)"
  ) %>%
  arrange(pol_b)

kable(ideology_table)
pol_b value_label Liberal Conservative NA
1 Extremely Liberal (1) 106 (100.0%) 0 (0.0%) 0 (0.0%)
2 Liberal (2) 173 (100.0%) 0 (0.0%) 0 (0.0%)
3 Slightly Liberal (3) 129 (100.0%) 0 (0.0%) 0 (0.0%)
4 Moderate (4) 224 (47.3%) 248 (52.3%) 2 (0.4%)
5 Slightly Conservative (5) 0 (0.0%) 158 (100.0%) 0 (0.0%)
6 Conservative (6) 0 (0.0%) 173 (100.0%) 0 (0.0%)
7 Extremely Conservative (7) 0 (0.0%) 125 (100.0%) 0 (0.0%)
NA NA 0 (0.0%) 0 (0.0%) 127 (100.0%)

Political Identity, Drive and Motivation

Break these down so we have all the measures that are used throughout. Specifically, we computed a series of new variables that are used in subsequent analyses or for error checking later. We show the code for these new variables and then the correlation matrix for all the variables of interest.

Code 
# conservative is our new primary political interest variable

# political party identity
# Mean of polcert_b and polmoral_b
dat$polStrength <- rowMeans(dat[, c("polcert_b", "polmoral_b")])

print(paste("Correlation (Political Certainty & Morality) =", cor(dat$polcert_b, dat$polmoral_b, use = "pairwise.complete.obs")))
[1] "Correlation (Political Certainty & Morality) = 0.707962678623325"
Code 
ggplot(dat, aes(x = polcert_b, y = polmoral_b)) +
  geom_smooth(method = "lm", se = FALSE) +
  geom_smooth() +
  geom_point(position = "jitter") +
  labs(x = "Political Certainty", y = "Political Morality") +
  theme_minimal()

Code 
# Combine two variables suppopRep and suppopDem into one variable.  If one is NA, use the other
# is your political drive more focused on supporting your own party or opposing the other party?
dat$PolDrive <- ifelse(is.na(dat$suppoppRep), dat$suppoppDem, dat$suppoppRep)
# higher values indicate that the respondent is more focused on supporting their own party

## PolDrive is a new variable that indicates drive to support own party

dat$polDrvSupOwnParty <- dat$PolDrive



hist(dat$PolDrive)

Code 
print(paste("Correlation (Political Drive & Strength) =", cor(dat$PolDrive, dat$polStrength)))
[1] "Correlation (Political Drive & Strength) = NA"
Code 
# First, calculate the medians for each PolDrive value
median_data <- dat %>%
  group_by(PolDrive) %>%
  summarize(median_strength = median(polStrength, na.rm = TRUE))

# Create the plot
ggplot() +
  # Add boxplots at each PolDrive value
  geom_boxplot(
    data = dat,
    aes(x = factor(PolDrive), y = polStrength, group = factor(PolDrive)),
    width = 0.6,
    fill = "lightblue",
    alpha = 0.7
  ) +
  
  # Add points to show the actual median values
  geom_point(
    data = median_data,
    aes(x = factor(PolDrive), y = median_strength),
    size = 3,
    color = "darkred"
  ) +
  
  # Add smooth curve through the medians
  geom_smooth(
    data = median_data,
    aes(x = as.numeric(as.character(PolDrive)), y = median_strength),
    method = "loess",
    se = FALSE,
    color = "darkred",
    size = 1.5
  ) +
  
  # Customize labels and theme to match your original plot
  labs(
    x = "Political Drive to Support Own Party", 
    y = "Politically Motivated"
  ) +
  theme_minimal()

Expectation of Openness to Political Perspectives (Self vs. Others)

We computed openness to political perspectives using the items from the self and other measures with the means of multiple variables to create new variables that represented the expectation of openness to political perspectives. Then, we then computed the difference between the self and other expectations to examine any differences in openness of self versus others. The code for these new variables is below.

Code 
# expectation of self vs. others
self <- dat %>%
  select(SelfInterBene1:SIH2)
other <- dat %>%
  select(otherInterBene1:OtherSIH2)
self$selfTotal <- rowMeans(self)
other$otherTotal <- rowMeans(other)

kable(getQuests(self[,1:4]), col.names = c("Variable", "Label"))
Variable Label
SelfInterBene1 In the long term, I appreciate considering a different perspective.
OtherInterBene2 I think my political party is stronger when people share differing opinions.
SIH1 I am open to revising my important beliefs in the face of new information.
SIH2 I am willing to change my position on an important issue in the face of good reasons
Code 
kable(getQuests(other[,1:4]), col.names = c("Variable", "Label"))
Variable Label
otherInterBene1 In the long term, other people in my political party appreciate considering a different perspective.
otherInterBene2.0 Other people in my political party think my party is stronger when people share differing opinions.
OtherSIH1 Other people in my political party are open to revising their important beliefs in the face of new information.
OtherSIH2 Other people in my political party are willing to change their positions on an important issue in the face of good reasons

Psychometrics of Self

Code 
prettyalpha(alpha(self[,1:4]))

Cronbach Alpha:

RAW_ALPHA STD.ALPHA G6(SMC) AVERAGE_R S/N ASE MEAN SD MEDIAN_R
0.8 0.8 0.78 0.5 4.07 0.01 5.56 1.47 0.47

Alpha Values If Certain Items Were Dropped:

RAW_ALPHA STD.ALPHA G6(SMC) AVERAGE_R S/N ALPHA SE VAR.R MED.R
SelfInterBene1 0.78 0.77 0.73 0.53 3.44 0.01 0.03 0.47
OtherInterBene2 0.79 0.79 0.74 0.55 3.74 0.01 0.02 0.50
SIH1 0.68 0.71 0.62 0.45 2.42 0.01 0.00 0.44
SIH2 0.71 0.74 0.65 0.48 2.79 0.01 0.00 0.48

Item-Level Statistics:

N RAW.R STD.R R.COR R.DROP MEAN SD
SelfInterBene1 1304 0.72 0.76 0.63 0.56 4.78 1.49
OtherInterBene2 1304 0.69 0.75 0.60 0.53 4.93 1.44
SIH1 1299 0.88 0.85 0.81 0.73 6.19 2.21
SIH2 1299 0.85 0.81 0.76 0.68 6.36 2.18

Psychometrics of Other

Code 
prettyalpha(alpha(other[,1:4]))

Cronbach Alpha:

RAW_ALPHA STD.ALPHA G6(SMC) AVERAGE_R S/N ASE MEAN SD MEDIAN_R
0.82 0.82 0.8 0.54 4.71 0.01 5.05 1.42 0.52

Alpha Values If Certain Items Were Dropped:

RAW_ALPHA STD.ALPHA G6(SMC) AVERAGE_R S/N ALPHA SE VAR.R MED.R
otherInterBene1 0.79 0.79 0.74 0.56 3.77 0.01 0.02 0.50
otherInterBene2.0 0.80 0.80 0.75 0.57 4.01 0.01 0.01 0.54
OtherSIH1 0.72 0.75 0.67 0.50 2.99 0.01 0.00 0.47
OtherSIH2 0.75 0.78 0.70 0.54 3.46 0.01 0.00 0.54

Item-Level Statistics:

N RAW.R STD.R R.COR R.DROP MEAN SD
otherInterBene1 1304 0.75 0.79 0.69 0.61 4.41 1.41
otherInterBene2.0 1304 0.74 0.78 0.66 0.59 4.52 1.40
OtherSIH1 1296 0.88 0.85 0.80 0.73 5.60 2.06
OtherSIH2 1296 0.85 0.81 0.75 0.68 5.71 2.09

Relationship between Self and Other

Code 
print(paste("Correlation Between Self & Other = ", round(cor(self$selfTotal, other$otherTotal, use = "pairwise.complete.obs"),2)))
[1] "Correlation Between Self & Other =  0.58"
Code 
## add back to dat
dat$selfTotal <- self$selfTotal
dat$otherTotal <- other$otherTotal

ggplot(dat, aes(x = self$selfTotal, y = other$otherTotal)) +
  geom_smooth(method = "lm", se = FALSE) +
  geom_smooth() +
  geom_point(position = "jitter") +
  labs(x = "Self Expectation", y = "Other Expectation") +
  theme_minimal()

Effect size differences between self and other expectations.

Code 
# Effect size

ES <- (mean(dat$selfTotal, na.rm=T) - mean(dat$otherTotal, na.rm=T)) / sqrt(mean(sd(dat$otherTotal, na.rm=T)^2,sd(dat$selfTotal, na.rm=T)^2))
print(paste("Self-Other Openness Effect size =" ,round(ES,2)))
[1] "Self-Other Openness Effect size = 0.36"
Code 
library(ggplot2)
library(ggthemes)  # For additional themes

# Delta between self and other
dat$ExpDelta <- dat$selfTotal - dat$otherTotal

# Calculate some statistics for annotations
delta_mean <- mean(dat$ExpDelta, na.rm = TRUE)
delta_median <- median(dat$ExpDelta, na.rm = TRUE)
delta_sd <- sd(dat$ExpDelta, na.rm = TRUE)

# Create enhanced histogram
ggplot(dat, aes(x = ExpDelta)) +
  # Add density curve
  geom_density(fill = "skyblue", alpha = 0.4) +
  
  # Add histogram bars
  geom_histogram(
    aes(y = after_stat(density)),
    bins = 30,
    fill = "steelblue",
    color = "white",
    alpha = 0.7
  ) +
  
  # Add mean line
  geom_vline(
    xintercept = delta_mean,
    color = "firebrick",
    linetype = "dashed",
    size = 1
  ) +
  
  # Add median line
  geom_vline(
    xintercept = delta_median,
    color = "darkgreen",
    linetype = "dotted",
    size = 1
  ) +
  
  # Add zero reference line
  geom_vline(
    xintercept = 0,
    color = "black",
    linetype = "solid",
    size = 0.5,
    alpha = 0.7
  ) +
  
  # Add annotations for statistics
  annotate(
    "text",
    x = delta_mean + 0.5,
    y = 0.9 * max(density(dat$ExpDelta, na.rm = TRUE)$y),
    label = sprintf("Mean = %.2f", delta_mean),
    color = "firebrick",
    hjust = 0,
    size = 3.5
  ) +
  
  annotate(
    "text",
    x = delta_median - 0.5,
    y = 0.8 * max(density(dat$ExpDelta, na.rm = TRUE)$y),
    label = sprintf("Median = %.2f", delta_median),
    color = "darkgreen",
    hjust = 1,
    size = 3.5
  ) +
  
  # Add rug plot at bottom
  geom_rug(alpha = 0.3, color = "steelblue") +
  
  # Customize labels and title
  labs(
    title = "Distribution of Self-Other Expectation Differences",
    subtitle = sprintf("Mean = %.2f, Median = %.2f, SD = %.2f", 
                       delta_mean, delta_median, delta_sd),
    x = "Difference (Self - Other)",
    y = "Density",
    caption = "Note: Positive values indicate higher self expectations relative to others"
  ) +
  
  # Apply a clean theme
  theme_minimal() +
  
  # Custom theme elements
  theme(
    plot.title = element_text(face = "bold", size = 14),
    plot.subtitle = element_text(size = 11, color = "gray30"),
    plot.caption = element_text(face = "italic", size = 9),
    axis.title = element_text(face = "bold"),
    panel.grid.minor = element_blank(),
    panel.grid.major.x = element_blank()
  )

Distribution of Self-Other expectation differences, with density curve overlay

Five-Dimensional Curiosity Scale-Revised (5DCR)

The following code is used to compute the Five-Dimensional Curiosity Scale-Revised (5DCR) variables. Each wave had data for the 5DCR. We also computed the means for each of the five dimensions of curiosity. The code below shows how we did these steps. Further, we computed the correlation matrix for the 5DCR variables and other relevant variables. We also computed the means for each of the five dimensions of curiosity. The code below shows how we did these steps. Finally, we computed the correlation matrix for the 5DCR variables and other relevant variables.

We also computed the means for each of the five dimensions of curiosity. The code below shows how we did these steps. Further, we computed the correlation matrix for the 5DCR variables and other relevant variables. We also computed the means for each of the five dimensions of curiosity. The code below shows how we did these steps. Finally, we computed the correlation matrix for the 5DCR variables and other relevant variables.

Variable Item Wording
JE1 I view novel political perspectives as an opportunity to grow and learn.
JE2 I seek out political information in hopes of having to think in depth.
JE3 I enjoy learning about political issues and perspectives that are unfamiliar to me.
JE4 I find it fascinating to learn new information about politics.
DS1 Thinking about solutions to difficult political issues can keep me awake at night.
DS2 I can spend hours on a single political problem because I just can't rest without knowing the answer.
DS3 I feel frustrated if I can't figure out the solution to a political problem, so I work even harder to solve it.
DS4 I work relentlessly at political problems that I feel must be solved.
ST1 I am uninterested in seeking out new political information if it will cause me discomfort
ST2 I cannot handle the stress that comes from listening to political perspectives that differ from my own.
ST3 I find it hard to engage with new political perspectives when I lack confidence in my positions.
ST4 It is difficult to concentrate on political information when there is a possibility that I will be taken by surprise.
TS1 Taking risks in how I express my political views is exciting to me.
TS2 When I have free time, I want to explore political ideas and positions on things that are a little controversial.
TS3 Jumping into political conversations without fully thinking through what I will say is more appealing than planning ahead of time.
TS4 I prefer friends who are excitingly unpredictable when it comes to their political views.
GSC1 I ask a lot of questions to figure out where other people stand politically.
GSC2 When talking to someone who is excited about a political topic, I am curious to find out why.
GSC3 When talking to someone, I try to discover interesting details about their political views.
GSC4 I like finding out why people behave the way they do politically.
Openness persTot selfTotal otherTotal
JE 0.52 0.36 0.49 0.42
DS 0.30 0.47 0.19 0.31
ST 0.03 0.29 0.02 0.19
TS 0.33 0.50 0.20 0.34
GSC 0.51 0.51 0.32 0.34
CSC 0.46 0.55 0.25 0.32
Psychometric Properties of Five-Dimensional Curiosity Scale-Revised (5DCR)
Descriptives
Reliability
Study Scale Mean SD Cronbach's α Min Item-Total r Max Item-Total r N
Study 1
Study 1 DS 3.42 1.68 0.916 0.75 0.84 1242
Study 1 GSC 3.94 1.60 0.905 0.73 0.84 1242
Study 1 JE 4.45 1.39 0.877 0.65 0.78 1242
Study 1 ST 3.41 1.47 0.842 0.58 0.74 1242
Study 1 TS 3.49 1.51 0.852 0.67 0.72 1242
Study 2
Study 2 DS 2.71 1.53 0.920 0.75 0.86 423
Study 2 GSC 4.08 1.63 0.906 0.75 0.85 423
Study 2 JE 4.58 1.38 0.883 0.60 0.83 423
Study 2 ST 3.03 1.24 0.725 0.43 0.57 423
Study 2 TS 2.78 1.32 0.795 0.57 0.65 423
Study 3a
Study 3a DS 2.61 1.47 0.913 0.71 0.87 647
Study 3a GSC 3.77 1.54 0.890 0.71 0.82 647
Study 3a JE 4.54 1.39 0.887 0.60 0.85 647
Study 3a ST 2.78 1.29 0.795 0.53 0.70 647
Study 3a TS 2.69 1.25 0.774 0.53 0.62 647
Study 3b
Study 3b DS 2.62 1.46 0.920 0.75 0.85 590
Study 3b GSC 4.17 1.48 0.893 0.71 0.82 590
Study 3b JE 4.69 1.37 0.893 0.64 0.86 590
Study 3b ST 3.01 1.26 0.769 0.52 0.63 590
Study 3b TS 2.82 1.30 0.806 0.56 0.70 590
* Note: Item-Total r refers to corrected item-total correlations.

ANALYSES & RESULTS

We used three sequential studies to address three research questions.

Question 1 (Study 1): Does curiosity predict positive attitudes toward diverse political viewpoints (i.e., open-mindedness) and a willingness to change personal beliefs (i.e., intellectual humility)?

Curiosity may be a mutable treatment target but only if the relationship between curiosity and these important outcomes remains both positive and reliable.

We defined open-mindedness here to be context specific - namely political openness - and as the mean of the items related to how they value openness to other perspectives (see table below). We then pose our question and a simple linear model ought to suffice.

Code 
# Advanced correlation plot for the supplement

# Load required libraries
library(ggplot2)
library(reshape2)
library(dplyr)
library(viridis)


# Example usage for the paper:
q1dat <- dat %>%
  select(JE, DS, ST, TS, GSC, selfTotal, otherTotal, Openness, persTot)

# Generate the enhanced correlation plot

curiosity_dims <- q1dat %>% select(JE, DS, ST, TS, GSC)
outcome_vars <- q1dat %>% select(selfTotal, otherTotal, Openness, persTot)

# Calculate correlations between these two sets
cross_cors <- cor(curiosity_dims, outcome_vars, use = "pairwise.complete.obs")

# Convert to long format
cross_cors_long <- melt(cross_cors)
names(cross_cors_long) <- c("Curiosity_Dimension", "Outcome_Measure", "Correlation")

# Create focused correlation plot
ggplot(data = cross_cors_long, 
       aes(x = Curiosity_Dimension, y = Outcome_Measure, fill = Correlation)) +
  geom_tile() +
  scale_fill_gradient2(
    low = "#2166AC",     # Dark blue for strong negative correlations
    mid = "white",       # White for zero correlations
    high = "#B2182B",    # Dark red for strong positive correlations
    midpoint = 0,
    limits = c(-1, 1)
  ) +
  geom_text(aes(label = sprintf("%.2f", Correlation)), 
            color = ifelse(abs(cross_cors_long$Correlation) > 0.5, "white", "black"), 
            size = 4) +
  theme_minimal() +
  theme(axis.text.x = element_text(angle = 0),
        axis.title = element_blank(),
        panel.grid = element_blank()) +
  coord_fixed() +
  labs(title = "Correlations Between Curiosity Dimensions and Outcome Measures",
       subtitle = "Shows how each curiosity dimension relates to openness measures",
       fill = "Correlation")

Code 
# Save this focused plot
ggsave("curiosity_outcomes_correlations.png", width = 8, height = 6, dpi = 300)

Alternative Models

Below, we rearrange the data into a long (multiple record) format to facilitate the analysis of curiosity and self-reported openness via a graphical analysis and linear mixed effect modeling. Here, the variable Score represents the actual values reported by the participants for each curiosity dimension (JE, DS, ST, TS, GSC, CSC) and the variable Curiosity represents the type of curiosity dimension. The selfTotal and otherTotal variables represent the two self-reported variables concerning openness to political perspectives. We analyzed those variables below in greater detail.

Score selfTotal otherTotal
Score 1.00 0.24 0.31
selfTotal 0.24 1.00 0.58
otherTotal 0.31 0.58 1.00

Linear Models

We tested a series of linear models in increasing complexity. First, we estimated the effects for selfTotal and otherTotal separately as dependent variables for all tests. Second, we began with unconditional models whereby each test increased in terms of complexity and, as such, decreased in parsimony. Our aim at the end was to select the most parsimonious model and report it. Our results of these sequential steps are posted below.

The models we tested are as follows:

  1. Linear Models (lm1/lm2): These models estimate the individual values of the dependent variable (selfTotal or otherTotal) conditioned on the overall curiosity score and the subfactor (i.e., curiosity factor scores such as JE - Joyous Exploration). This is a simple model that is certainly wrong but it is simple to examine for obvious problems.

  2. Mixed Models (lme0s/lme0o): These models estimate the individual values of the dependent variable (selfTotal or otherTotal) conditioned on the overall curiosity score and the subfactor but allowing the means by subfactor to vary. These simpler mixed effects models now take into consideration the nesting and crossed effects in the model. These models are now more complex than the initial linear models but they are not the most complex models we can estimate.

  3. Mixed Models with Random Slopes (lme1s/lme1o): These models estimate the individual values of the dependent variable (selfTotal or otherTotal) conditioned on the overall curiosity score and the subfactor but allowing the means by subfactor to vary and allowing the slopes to vary as well. These models are now more complex than the previous mixed effects models but they are still not the most complex models we can estimate.

  4. Mixed Models with Random Slopes and Intercepts (lme2s/lme2o): These models estimate the individual values of the dependent variable (selfTotal or otherTotal) conditioned on the overall curiosity score and the subfactor but allowing the means by subfactor to vary and allowing the slopes to vary as well. These models are now more complex than the previous mixed effects models but they are still not the most complex models we can estimate.

Code 
# Create a combined table with model descriptions
model_descriptions <- data.frame(
  Model = c("lm1/lm2", "lme0s/lme0o", "lme1s/lme1o", "lme2s/lme2o"),
  Description = c(
    "Linear model with Score, Curiosity, and their interaction",
    "Mixed model with Score as fixed effect and random intercept for Curiosity",
    "Mixed model with Score as fixed effect and random slope and intercept for Curiosity",
    "Mixed model with Score, id, and their interaction as fixed effects, and random intercept for Curiosity"
  )
)

model_descriptions %>%
  kable(format = "markdown") %>%
  kable_styling()
Model Description
lm1/lm2 Linear model with Score, Curiosity, and their interaction
lme0s/lme0o Mixed model with Score as fixed effect and random intercept for Curiosity
lme1s/lme1o Mixed model with Score as fixed effect and random slope and intercept for Curiosity
lme2s/lme2o Mixed model with Score, id, and their interaction as fixed effects, and random intercept for Curiosity

Model Results

Code 
lm1 <- lm(selfTotal ~ Score*Curiosity, data = q1dat)
lm2 <- lm(otherTotal ~ Score*Curiosity, data = q1dat)
tab_model(lm1, lm2)
  selfTotal otherTotal
Predictors Estimates CI p Estimates CI p
(Intercept) 4.72 4.52 – 4.92 <0.001 4.00 3.81 – 4.19 <0.001
Score 0.23 0.18 – 0.27 <0.001 0.28 0.23 – 0.33 <0.001
Curiosity [DS] 0.28 0.01 – 0.55 0.041 0.17 -0.08 – 0.42 0.190
Curiosity [GSC] -0.28 -0.57 – 0.01 0.057 -0.13 -0.40 – 0.14 0.349
Curiosity [JE] -1.45 -1.78 – -1.12 <0.001 -0.83 -1.15 – -0.52 <0.001
Curiosity [ST] 0.78 0.50 – 1.06 <0.001 0.45 0.18 – 0.71 0.001
Curiosity [TS] 0.18 -0.10 – 0.46 0.204 -0.03 -0.30 – 0.24 0.816
Score × Curiosity [DS] -0.06 -0.12 – 0.01 0.103 -0.02 -0.08 – 0.05 0.584
Score × Curiosity [GSC] 0.06 -0.01 – 0.13 0.070 0.02 -0.04 – 0.09 0.475
Score × Curiosity [JE] 0.29 0.22 – 0.37 <0.001 0.15 0.08 – 0.22 <0.001
Score × Curiosity [ST] -0.20 -0.27 – -0.13 <0.001 -0.10 -0.17 – -0.03 0.005
Score × Curiosity [TS] -0.03 -0.10 – 0.04 0.383 0.03 -0.03 – 0.10 0.314
Observations 7452 7452
R2 / R2 adjusted 0.080 / 0.079 0.107 / 0.106
Code 
lme0s <- lmer(selfTotal ~ Score + (1|Curiosity), data = q1dat)
lme0o <- lmer(otherTotal ~ Score + (1|Curiosity), data = q1dat)
tab_model(lme0s, lme0o)
  selfTotal otherTotal
Predictors Estimates CI p Estimates CI p
(Intercept) 4.72 4.61 – 4.83 <0.001 3.98 3.86 – 4.10 <0.001
Score 0.23 0.21 – 0.25 <0.001 0.29 0.27 – 0.31 <0.001
Random Effects
σ2 2.03 1.80
τ00 0.01 Curiosity 0.01 Curiosity
ICC 0.00 0.01
N 6 Curiosity 6 Curiosity
Observations 7452 7452
Marginal R2 / Conditional R2 0.061 / 0.064 0.105 / 0.111
Code 
# Linear Model
lme1s <- lmer(selfTotal ~ Score + (Score | Curiosity), data = q1dat)
lme1o <- lmer(otherTotal ~ Score + (Score | Curiosity), data = q1dat)
tab_model(lme1s, lme1o)
  selfTotal otherTotal
Predictors Estimates CI p Estimates CI p
(Intercept) 4.64 4.03 – 5.25 <0.001 3.94 3.61 – 4.28 <0.001
Score 0.24 0.11 – 0.37 <0.001 0.29 0.23 – 0.35 <0.001
Random Effects
σ2 1.99 1.79
τ00 0.57 Curiosity 0.16 Curiosity
τ11 0.03 Curiosity.Score 0.01 Curiosity.Score
ρ01 -1.00 Curiosity -0.99 Curiosity
ICC 0.04 0.02
N 6 Curiosity 6 Curiosity
Observations 7452 7452
Marginal R2 / Conditional R2 0.064 / 0.105 0.107 / 0.123
Code 
lme2s <- lmer(selfTotal ~ Score*id + (1|Curiosity), data = q1dat)
lme2o <- lmer(otherTotal ~ Score*id + (1|Curiosity), data = q1dat)
tab_model(lme2s, lme2o)
  selfTotal otherTotal
Predictors Estimates CI p Estimates CI p
(Intercept) 4.65 4.47 – 4.83 <0.001 4.12 3.94 – 4.30 <0.001
Score 0.22 0.18 – 0.27 <0.001 0.26 0.22 – 0.30 <0.001
id 0.00 -0.00 – 0.00 0.324 -0.00 -0.00 – 0.00 0.052
Score × id 0.00 -0.00 – 0.00 0.827 0.00 -0.00 – 0.00 0.062
Random Effects
σ2 2.03 1.80
τ00 0.01 Curiosity 0.01 Curiosity
ICC 0.00 0.01
N 6 Curiosity 6 Curiosity
Observations 7452 7452
Marginal R2 / Conditional R2 0.062 / 0.065 0.105 / 0.112

Model Fit Indices

Both lme1s and lme1o are the most parsimonious models for selfTotal and otherTotal, respectively. We can use AIC and BIC to compare the models. The table below shows the AIC and BIC values for each model.

Code 
# Load required packages
library(broom)
library(broom.mixed)  # For handling mixed models
library(dplyr)
library(kableExtra)   # For nice table formatting
library(lme4)         # Ensure this is loaded for the mixed models

# Function to extract AIC and BIC from a model
get_fit_indices <- function(model, model_name) {
  # Define dependent variable based on model name instead of formula
  dependent <- if(grepl("[s]$", model_name)) "selfTotal" else "otherTotal"
  
  if(inherits(model, "lm") || inherits(model, "lmerMod")) {
    data.frame(
      Model = model_name,
      AIC = AIC(model),
      BIC = BIC(model),
      Dependent = dependent
    )
  } else {
    stop("Unsupported model type")
  }
}

# Create a list of models with their names
models_list <- list(
  "lm1" = lm1,
  "lm2" = lm2,
  "lme0s" = lme0s,
  "lme0o" = lme0o,
  "lme1s" = lme1s,
  "lme1o" = lme1o,
  "lme2s" = lme2s,
  "lme2o" = lme2o
)

# Extract fit indices for all models
fit_indices <- lapply(names(models_list), function(name) {
  get_fit_indices(models_list[[name]], name)
}) %>% 
  bind_rows()

# Special case for lm1 and lm2 which don't follow the same naming pattern
fit_indices$Dependent[fit_indices$Model == "lm1"] <- "selfTotal"
fit_indices$Dependent[fit_indices$Model == "lm2"] <- "otherTotal"

# Create separate tables by dependent variable
fit_indices_self <- fit_indices %>%
  filter(Dependent == "selfTotal") %>%
  arrange(BIC) %>%
  select(-Dependent)

fit_indices_other <- fit_indices %>%
  filter(Dependent == "otherTotal") %>%
  arrange(BIC) %>%
  select(-Dependent)

# Print the tables
fit_indices_self %>%
  kable(format = "markdown", digits = 2) %>%
  print()  # Using print() instead of kable_styling for more reliable output
Model AIC BIC
lme1s 26307.04 26348.53
lm1 26272.71 26362.63
lme0s 26452.22 26479.88
lme2s 26483.95 26525.44
Code 
fit_indices_other %>%
  kable(format = "markdown", digits = 2) %>%
  print()  # Using print() instead of kable_styling for more reliable output
Model AIC BIC
lme1o 25514.32 25555.81
lme0o 25542.91 25570.57
lm2 25485.25 25575.17
lme2o 25580.83 25622.33

Question 2 (Study 1): Do people accurately gauge their fellow political party members’ attitudes toward diverse viewpoints (i.e., open-mindedness) and a willingness to change personal beliefs (i.e., intellectual humility)?

Any discrepancy between self-ratings and other ratings indicates the potential target for a wise intervention that helps adjust these discrepancies. The short answer is no. Yes, people hold themselves in very high esteem and higher than they hold their peers. We have evidence that the self reported openness is significantly higher than the reported openness for others - providing us with a reason to intervene.

Code 
# as stated in the manuscript, we will use the conservative_f variable as our primary political interest variable.  To do so, we need to rearrange the data.  Here, I do so in tidyverse style.

datTMP <- dat %>%
  select(id, 
         conservative_f, 
         polStrength, 
         polcert_b, 
         polmoral_b, 
         PolDrive, 
         selfTotal, 
         otherTotal, 
         ExpDelta)

# create long format where each row has a participant and a new variable for self or other
datTMP <- datTMP %>%
  pivot_longer(cols = c(selfTotal, otherTotal), 
               names_to = "SelfvsOther", 
               values_to = "ExpectationValue")

aov0 <- aov(ExpectationValue ~ SelfvsOther, 
            data = datTMP)
tab_model(aov0)
  ExpectationValue
Predictors p
SelfvsOther <0.001
Residuals
Observations 2595
R2 / R2 adjusted 0.030 / 0.029

T-test

Code 
#t.test(dat$selfTotal, dat$otherTotal, paired = TRUE)

# tidy output of t.test
t.test(dat$selfTotal, dat$otherTotal, paired = TRUE) %>%
  tidy() %>%
  kable(format = "markdown", digits = 2) %>%
  kable_styling()
estimate statistic p.value parameter conf.low conf.high method alternative
0.51 13.81 0 1292 0.44 0.58 Paired t-test two.sided

Linear mixed effects models

Code 
library(lme4)
library(lmerTest)
lme0 <- lmer(ExpectationValue ~ SelfvsOther + (1|id), data = datTMP)
lme1 <- lmer(ExpectationValue ~ SelfvsOther * conservative_f + (1|id), data = datTMP)
tab_model(lme0, lme1)
  ExpectationValue ExpectationValue
Predictors Estimates CI p Estimates CI p
(Intercept) 5.06 4.98 – 5.14 <0.001 5.18 5.07 – 5.29 <0.001
SelfvsOther [selfTotal] 0.51 0.44 – 0.58 <0.001 0.56 0.45 – 0.66 <0.001
conservative f
[Conservative]		 -0.24 -0.39 – -0.08 0.003
SelfvsOther [selfTotal] ×
conservative f
[Conservative]		 -0.10 -0.24 – 0.05 0.196
Random Effects
σ2 0.88 0.88
τ00 1.21 id 1.20 id
ICC 0.58 0.58
N 1302 id 1302 id
Observations 2595 2595
Marginal R2 / Conditional R2 0.030 / 0.592 0.039 / 0.592

Some linear models

Code 
# ANOVA
aov1 <- aov(selfTotal ~ polStrength * conservative_f, data = dat)
aov2 <- aov(otherTotal ~ polStrength * conservative_f, data = dat)
tab_model(aov1, aov2)
  selfTotal otherTotal
Predictors p p
polStrength <0.001 <0.001
conservative_f <0.001 <0.001
polStrength:conservative_f <0.001 0.003
Residuals
Observations 1299 1296
R2 / R2 adjusted 0.166 / 0.164 0.111 / 0.109

So yeah, they do.

Question 3 (Studies 2 and 3): Can a “wise intervention” effectively boost people’s political curiosity, open-mindedness, and intellectual humility?

A simple intervention that targets discrepant views might lead to greater curiosity and, in turn, open-mindedness and humility. We ran several models to address this question. We first ran a structural equation model (SEM) on cross-sectional data to test the relationship between political curiosity and political openness (S1). We then manipulated political curiosity to see if we could change political openness (S2). Finally, we tested if the effect persisted over time (S3). The results are below.

Question 3a: Do these effects come out in a cross-sectional design? (S1)

YES. Yes, they do.

Estimator: ML

Converged: TRUE

Iterations: 15

Original Sample Size: 1465

Effective Sample Size: 1238

Fit Indices:

NPAR CHISQ DF PVALUE CFI TLI NNFI NFI RMSEA SRMR AIC BIC
Values 6 0 0 NA 1 1 1 1 0 0 12217.67 12248.4

Parameter Estimates:

LHS OP RHS STD.ALL EST SE Z PVALUE
Openness ~ JE 0.325 0.321 0.030 10.798 0
Openness ~ GSC 0.303 0.260 0.026 10.069 0
JE ~~ GSC 0.628 1.399 0.075 18.715 0
Openness ~~ Openness 0.679 1.279 0.051 24.880 0
JE ~~ JE 1.000 1.933 0.078 24.880 0
GSC ~~ GSC 1.000 2.565 0.103 24.880 0

Here are the results of the CFA.

Code 
h3fig1 <- lavaanPlot(fit1, 
           coefs=TRUE, 
           stars=TRUE, 
           digits=2, 
           stand=TRUE, 
           covs=TRUE,
           graph_options=list(rankdir = "LR")) # doesn't show when quarto file rendered
# Error:  TypeError: Assignmnet to constant variable.
save_png(h3fig1, "H3fig1.png")

#lm3biggie <- lm(learnTot ~ Condition, data = dat3)
#summary(lm3biggie)

Question 3b: Can we Manipulate Political Curiosity?

We used the second study to test a manipulation of political curiosity. We then tested if the manipulation changed political openness. The results are below.

Code 
m2 <- '
  Openness ~ JE + GSC + Condition
  JE ~ Condition
  GSC ~ Condition
  JE ~~ GSC
'

dat2$Openness <- rowMeans(dat2[, c("learn1", "learn2")])
dat2$persTot <- rowMeans(dat2[, c("persuade1", "persuade2")])

#print(paste("The variable CondNum is in the dataset:", "CondNum" %in% #names(dat2w5DCR)))

fit2 <- sem(m2, data = dat2)
prettylavaan(fit2, output_format = "asis")

Estimator: ML

Converged: TRUE

Iterations: 13

Original Sample Size: 466

Effective Sample Size: 421

Fit Indices:

NPAR CHISQ DF PVALUE CFI TLI NNFI NFI RMSEA SRMR AIC BIC
Values 9 0 0 NA 1 1 1 1 0 0 3844.445 3880.829

Parameter Estimates:

LHS OP RHS STD.ALL EST SE Z PVALUE
Openness ~ JE 0.181 0.123 0.042 2.925 0.003
Openness ~ GSC 0.334 0.200 0.037 5.421 0.000
Openness ~ Condition 0.073 0.143 0.083 1.722 0.085
JE ~ Condition 0.112 0.318 0.138 2.309 0.021
GSC ~ Condition 0.109 0.354 0.158 2.240 0.025
JE ~~ GSC 0.724 1.655 0.138 12.030 0.000
Openness ~~ Openness 0.754 0.714 0.049 14.509 0.000
JE ~~ JE 0.987 1.997 0.138 14.509 0.000
GSC ~~ GSC 0.988 2.619 0.181 14.509 0.000
Condition ~~ Condition 1.000 0.250 0.000 NA NA
Code 
#summary(fit2, fit.measures = TRUE)

m2med <- '
  # a paths
  JE ~ aJ * Condition
  GSC ~ aG * Condition
  
  # b paths
  Openness ~ bJ * JE + bG * GSC

  # c prime path
  Openness ~ cp * Condition
  
  # indirect and total effects
  indirect_JE := aJ * bJ
  indirect_GSC := aG * bG
  total_JE := cp + indirect_JE
  total_GSC := cp + indirect_GSC
'

fit2med <- sem(m2med, data = dat2)
prettylavaan(fit2med, output_format = "asis")

Estimator: ML

Converged: TRUE

Iterations: 1

Original Sample Size: 466

Effective Sample Size: 421

Fit Indices:

NPAR CHISQ DF PVALUE CFI TLI NNFI NFI RMSEA SRMR AIC BIC
Values 8 312.354 1 0 0.285 -3.29 -3.29 0.292 0.86 0.243 4154.8 4187.141

Parameter Estimates:

LHS OP RHS STD.ALL EST SE Z PVALUE
JE ~ Condition 0.112 0.318 0.138 2.309 0.021
GSC ~ Condition 0.109 0.354 0.158 2.240 0.025
Openness ~ JE 0.189 0.123 0.029 4.238 0.000
Openness ~ GSC 0.350 0.200 0.025 7.856 0.000
Openness ~ Condition 0.077 0.143 0.083 1.713 0.087
JE ~~ JE 0.987 1.997 0.138 14.509 0.000
GSC ~~ GSC 0.988 2.619 0.181 14.509 0.000
Openness ~~ Openness 0.825 0.714 0.049 14.509 0.000
Condition ~~ Condition 1.000 0.250 0.000 NA NA
Code 
#summary(fit2med, fit.measures = TRUE, standardized = TRUE)

#fitMeasures(fit2, c("cfi", "tli", "rmsea", "srmr", "aic", "bic"))
Means and Standard Deviations by Condition
Openness
Joyous Exploration
General Social Curiosity
Condition Mean SD Mean SD Mean SD
Control 5.35 1.01 3.99 1.51 3.97 1.70
Intervention 5.61 0.92 4.32 1.31 4.33 1.53
Code 
h3fig2 <- lavaanPlot(fit2, 
           coefs=TRUE, 
           stars=TRUE, 
           digits=2, 
           stand=TRUE, 
           covs=TRUE,
           graph_options=list(rankdir = "LR")) # doesn't show when quarto file rendered
# Error:  TypeError: Assignmnet to constant variable.
save_png(h3fig2, "H3fig2.png")

Question 3c: Does the effect persist?

Finally, we tested the lasting effects of the manipulation. The results are below.

Code 
m3 <- '
  Openness2 ~ JE.2 + GSC2 + Ctl_v_Int + Ctl_v_AttC
  JE.2 ~ Ctl_v_Int + Ctl_v_AttC
  GSC.2 ~ Ctl_v_Int + Ctl_v_AttC
  JE.2 ~~ GSC.2
'


dat3$JE.2 <- dat3$JEb
dat3$GSC.2 <- dat3$GSCb

dat3$Condition <- as.factor(dat3$Condition)
levels(dat3$Condition)# <- c("Control", "Curious")

[1] “Control” “ControlAss” “Intervention”

Code 
dat3$Condition <- unclass(dat3$Condition) - 1

dat3$Ctl_v_Int <- ifelse(dat3$Condition == 2, 1, 0)
dat3$Ctl_v_AttC <- ifelse(dat3$Condition == 1, 1, 0)

dat3$Openness <- rowMeans(dat3[, c("learn1.x", "learn2.x")])
dat3$persTot <- rowMeans(dat3[, c("persuade1.x", "persuade2.x")])

dat3$Openness2 <- rowMeans(dat3[, c("learn1.y", "learn2.y")])
dat3$persTot2 <- rowMeans(dat3[, c("persuade1.y", "persuade2.y")])

fit3 <- sem(m3, data = dat3)
prettylavaan(fit3, output_format = "asis")

Estimator: ML

Converged: TRUE

Iterations: 29

Original Sample Size: 651

Effective Sample Size: 585

Fit Indices:

NPAR CHISQ DF PVALUE CFI TLI NNFI NFI RMSEA SRMR AIC BIC
Values 13 275.886 2 0 0.657 -1.06 -1.06 0.659 0.484 0.179 5488.243 5545.074

Parameter Estimates:

LHS OP RHS STD.ALL EST SE Z PVALUE
Openness2 ~ JE.2 0.444 0.366 0.030 12.140 0.000
Openness2 ~ GSC2 0.106 0.069 0.023 3.028 0.002
Openness2 ~ Ctl_v_Int 0.093 0.226 0.104 2.176 0.030
Openness2 ~ Ctl_v_AttC 0.018 0.043 0.100 0.429 0.668
JE.2 ~ Ctl_v_Int 0.088 0.260 0.142 1.830 0.067
JE.2 ~ Ctl_v_AttC -0.024 -0.069 0.137 -0.504 0.614
GSC.2 ~ Ctl_v_Int 0.099 0.317 0.153 2.071 0.038
GSC.2 ~ Ctl_v_AttC 0.001 0.002 0.148 0.012 0.991
JE.2 ~~ GSC.2 0.623 1.258 0.098 12.790 0.000
Openness2 ~~ Openness2 0.775 0.993 0.058 17.103 0.000
JE.2 ~~ JE.2 0.990 1.871 0.109 17.103 0.000
GSC.2 ~~ GSC.2 0.990 2.177 0.127 17.103 0.000
Openness2 ~~ GSC.2 0.220 0.324 0.049 6.553 0.000
GSC2 ~~ GSC2 1.000 3.052 0.000 NA NA
GSC2 ~~ Ctl_v_Int 0.092 0.075 0.000 NA NA
GSC2 ~~ Ctl_v_AttC -0.017 -0.015 0.000 NA NA
Ctl_v_Int ~~ Ctl_v_Int 1.000 0.216 0.000 NA NA
Ctl_v_Int ~~ Ctl_v_AttC -0.515 -0.115 0.000 NA NA
Ctl_v_AttC ~~ Ctl_v_AttC 1.000 0.232 0.000 NA NA
Code 
dat3$JE.diff <- dat3$JE2 - dat3$JE # for later use perhaps?

#sum(table(dat3$Condition))
#table(dat3$Condition)
Means and Standard Deviations by Condition
Openness
Joyous Exploration
General Social Curiosity
Condition Mean SD Mean SD Mean SD
Control 5.20 1.11 4.38 1.68 4.00 1.82
Attention 5.22 1.17 4.40 1.48 4.11 1.64
WISE 5.55 1.19 4.32 1.77 4.35 1.79
Code 
library(gridExtra)

#dat3$cond.f <- factor(dat3$Condition, labels = c("Control", "Attention", "WISE"))

p1 <- ggplot(dat3, aes(x = cond.f, y = Openness2, fill = cond.f)) +
  geom_boxplot() +
  labs(x = "Condition", y = "Openness") +
  theme_minimal() + 
  theme(legend.position = "none") + 
  labs(x = "")

p2 <- ggplot(dat3, aes(x = cond.f, y = JE.2, fill = cond.f)) +
  geom_boxplot() +
  labs(x = "Condition", y = "Joyous Exploration") +
  theme_minimal() + 
  theme(legend.position = "none") + 
  labs(x = "")

p3 <- ggplot(dat3, aes(x = cond.f, y = GSC.2, fill = cond.f)) +
  geom_boxplot() +
  labs(x = "Condition", y = "General Social Curiosity") +
  theme_minimal() +
  theme(legend.position = "none") + 
  labs(x = "")

grid.arrange(p1, p2, p3, ncol = 1)

DATA DETAILS

Final Variable List

We selected only the relevant variables for the models we tested and evaluated for this paper. As such, we present the final list of variables by study along with the missing data diagnostics.

Code 
# Main variables used in analyses for Study 1
dat_variables <- c(
  # identifier
  "id",
  
  # Political ideology and party variables
  "pol_b", "pol_mod_b", "pol_party_b", "pol_inde_b",
  "conservative", "conservative_bin", "republican_b", 
  "conservative_f", "republican_f",
  
  # Political identity strength variables
  "polcert_b", "polmoral_b", "polStrength",
  
  # Political drive variables
  "suppoppRep", "suppoppDem", "PolDrive", "polDrvSupOwnParty",
  
  # Self vs other political openness variables
  "SelfInterBene1", "SIH2", # (and other self variables through SIH2)
  "otherInterBene1", "OtherSIH2", # (and other 'other' variables through OtherSIH2)
  "selfTotal", "otherTotal", "ExpDelta",
  
  # 5DCR curiosity dimensions
  "JE", "DS", "ST", "TS", "GSC", "CSC",
  
  # Learning and persuasion variables
  "learn1", "learn2", "Openness",
  "persuade1", "persuade2", "persTot"
)

# Create a selection for data summaries that only includes analyzed variables
dat_selection <- dat %>% select(all_of(dat_variables))

# Main variables used in analyses for Study 2
dat2_variables <- c(
  # identifier
  "id",
  
  # Experimental condition variable
  "Condition",
  
  # 5DCR curiosity dimensions
  "JE", "DS", "ST", "TS", "GSC",
  
  # Learning and persuasion variables
  "learn1", "learn2", "Openness",
  "persuade1", "persuade2", "persTot"
)

# Create a selection for data summaries that only includes analyzed variables
dat2_selection <- dat2 %>% select(all_of(dat2_variables))

# Main variables used in analyses for Study 3
dat3_variables <- c(
  # identifier
  "id",
  
  # Experimental condition variable
  "Condition",
  
  # 5DCR curiosity dimensions (pre-intervention)
  "JE", "DS", "ST", "TS", "GSC",
  
  # 5DCR curiosity dimensions (post-intervention)
  "JEb", "DSb", "STb", "TSb", "GSCb",
  "JE2", "GSC2", # (post-intervention computed variables)
  
  # Learning and persuasion variables (pre-intervention)
  "learn1.x", "learn2.x", "Openness",
  "persuade1.x", "persuade2.x", "persTot",
  
  # Learning and persuasion variables (post-intervention)
  "learn1.y", "learn2.y", "Openness2",
  "persuade1.y", "persuade2.y", "persTot2"
)

# Create a selection for data summaries that only includes analyzed variables
dat3_selection <- dat3 %>% select(all_of(dat3_variables))

Study 1 Variables

Code 
#kable(getQuests(dat[c(19:34,59:71)]), col.names = c("Variable", "Label"))

# d1 <- dat[c(19:34,59:71)]
# 
dfSummary(dat_selection[,-1],
          class = F,
          varnumbers = FALSE,
          display.labels = F,
          graph.col = T,
          graph.magnif = 0.85,
          valid.col = T,
          na.col=F,
          tmp.img.dir = "tmp",
          style = "grid",
          plain.ascii = F,
          silent = T,
          freq.silent = T)

Data Frame Summary

dat_selection

Dimensions: 1465 x 35
Duplicates: 129

Variable Label Stats / Values Freqs (% of Valid) Graph Valid
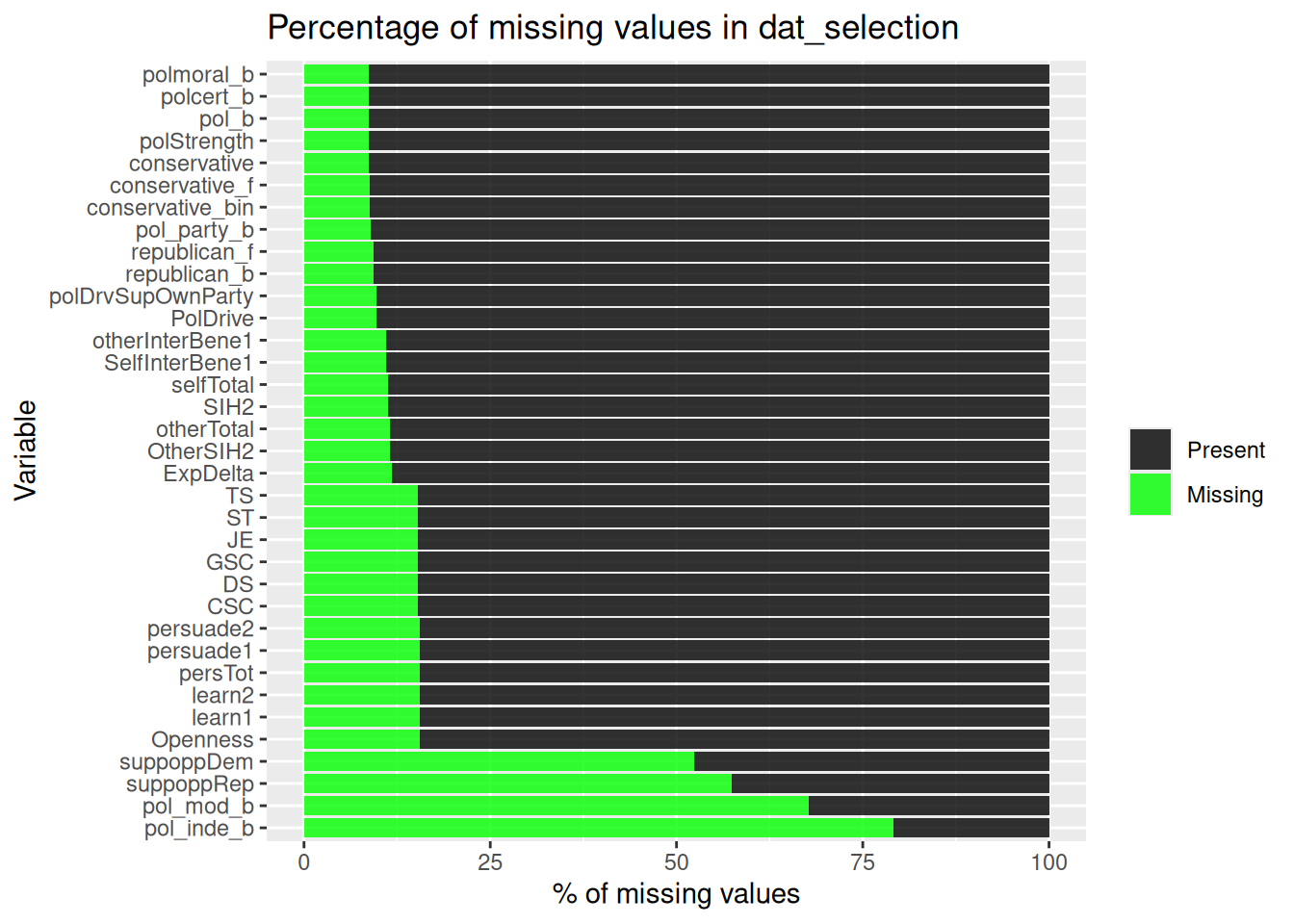
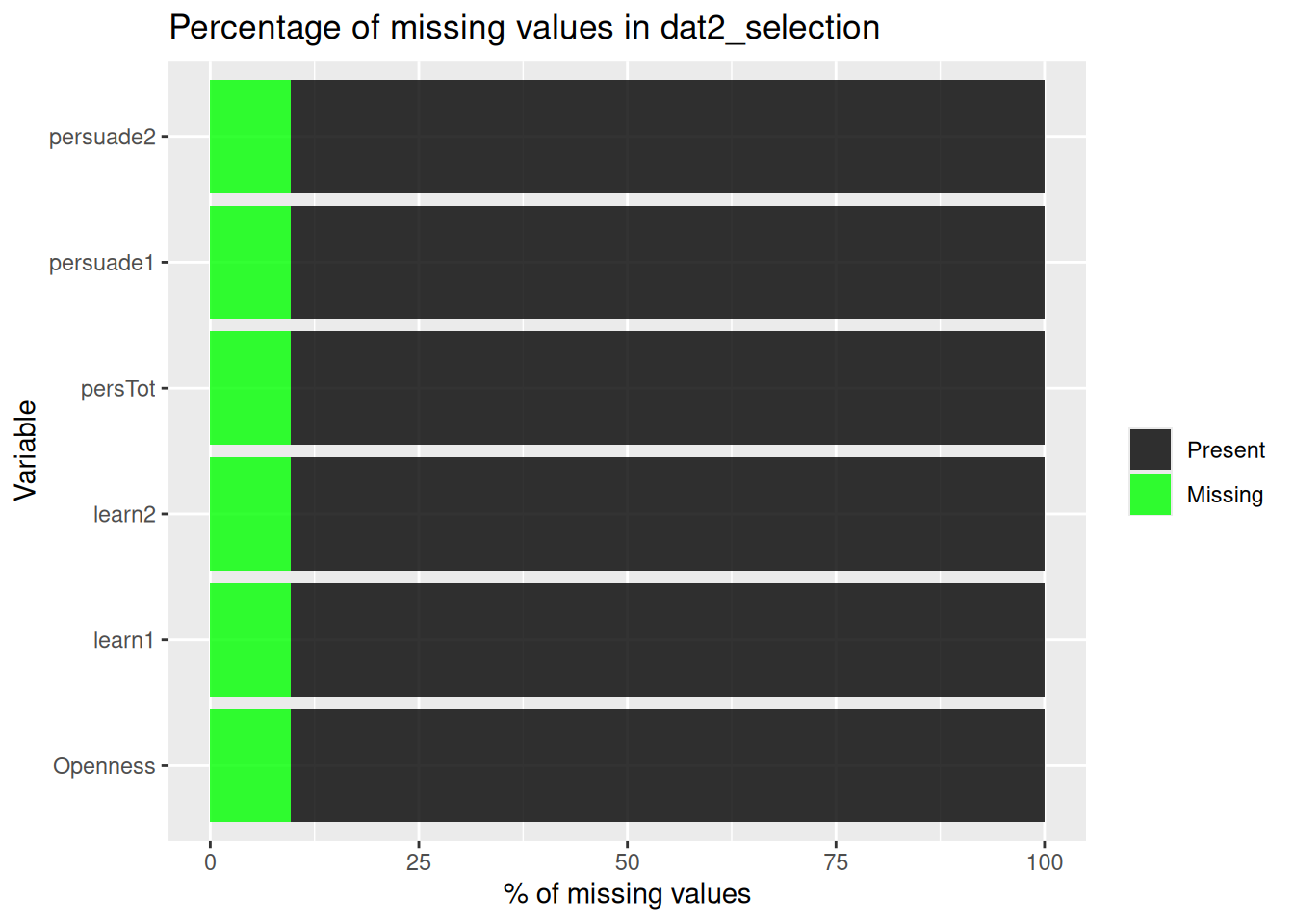
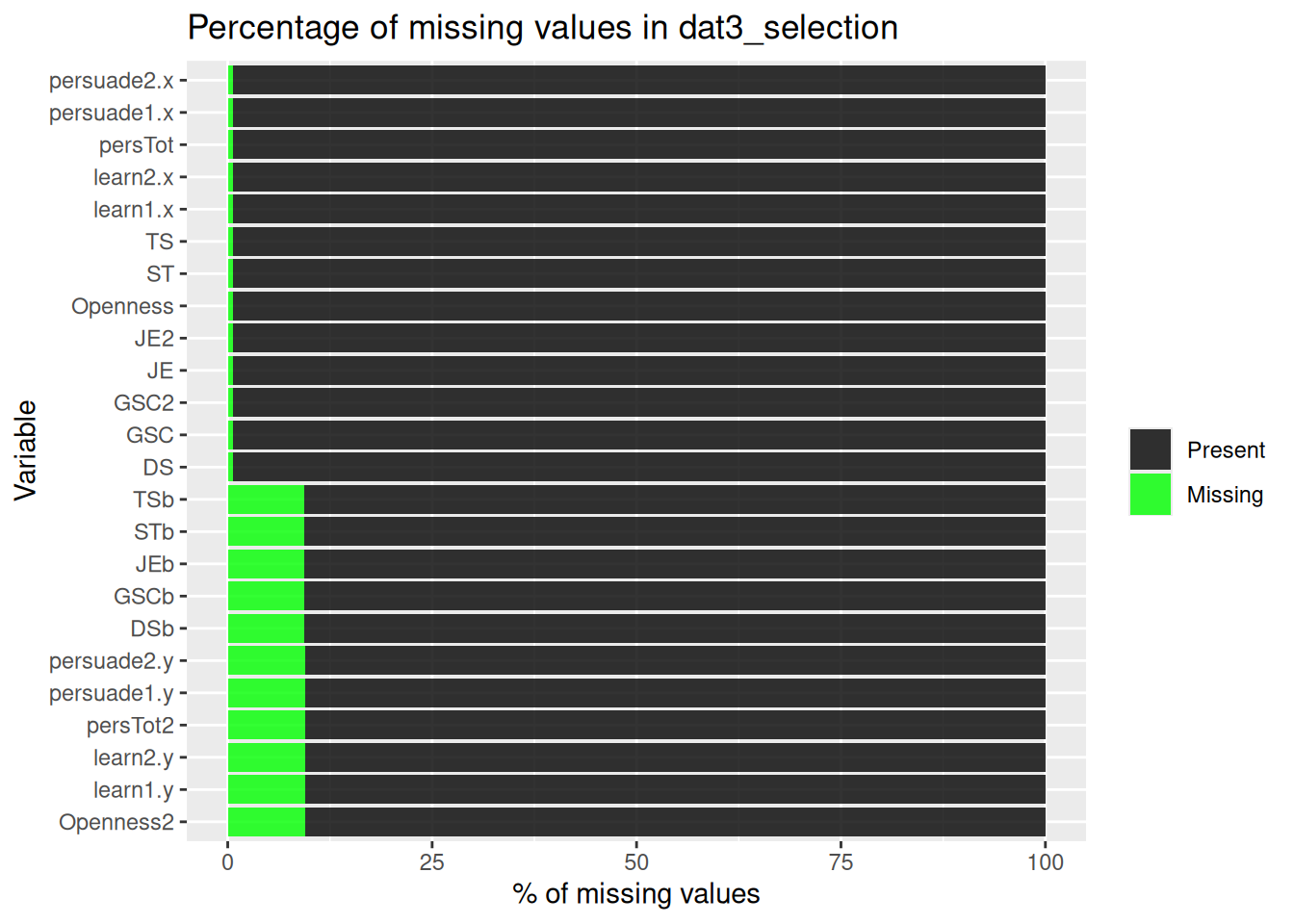
pol_b Political Ideology 1. [1] extremely liberal
2. [2] liberal
3. [3] somewhat liberal
4. [4] moderate/middle of th
5. [5] somewhat conservative
6. [6] conservative
7. [7] extremely conservativ		 106 ( 7.9%)
173 (12.9%)
129 ( 9.6%)
474 (35.4%)
158 (11.8%)
173 (12.9%)
125 ( 9.3%)		 1338
(91.3%)
pol_mod_b Liberal or Conservative 1. [1] Liberal
2. [2] Conservative		 224 (47.5%)
248 (52.5%)		 472
(32.2%)
pol_party_b Party Affilitation 1. [1] Strong Democrat
2. [2] Democrat
3. [3] Independent, leaning
4. [4] Independent
5. [5] Independent, leaning
6. [6] Republican
7. [7] Strong Republican		 162 (12.1%)
229 (17.2%)
157 (11.8%)
311 (23.3%)
140 (10.5%)
190 (14.2%)
145 (10.9%)		 1334
(91.1%)
pol_inde_b Democrat or Republican 1. [1] Democrat
2. [2] Republican		 152 (49.7%)
154 (50.3%)		 306
(20.9%)
conservative Political Ideology 1. [1] extremely liberal
2. [2] liberal
3. [3] somewhat liberal
4. [4] moderate/middle of th
5. [5] somewhat conservative
6. [6] conservative
7. [7] extremely conservativ		 106 ( 7.9%)
173 (12.9%)
129 ( 9.6%)
474 (35.4%)
158 (11.8%)
173 (12.9%)
125 ( 9.3%)		 1338
(91.3%)
conservative_bin Min : 0
Mean : 0.5
Max : 1		 0 : 632 (47.3%)
1 : 704 (52.7%)		 1336
(91.2%)
republican_b Min : 0
Mean : 0.5
Max : 1		 0 : 700 (52.7%)
1 : 629 (47.3%)		 1329
(90.7%)
conservative_f 1. Liberal
2. Conservative		 632 (47.3%)
704 (52.7%)		 1336
(91.2%)
republican_f 1. Democrat
2. Republican		 700 (52.7%)
629 (47.3%)		 1329
(90.7%)
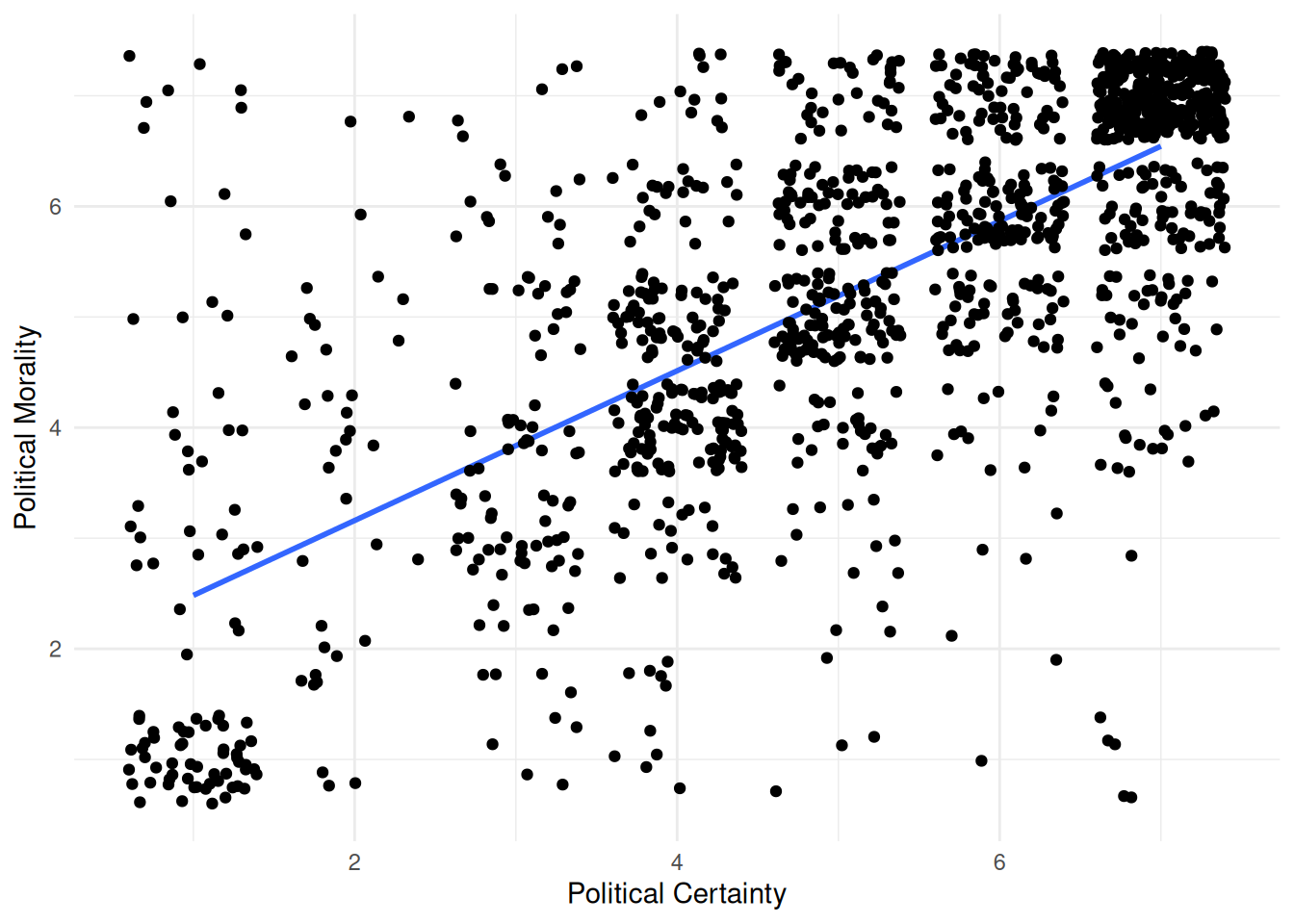
polcert_b How certain are you in your political ideology? 1. [1] 1
2. [2] 2
3. [3] 3
4. [4] 4
5. [5] 5
6. [6] 6
7. [7] 7		 93 ( 7.0%)
35 ( 2.6%)
98 ( 7.3%)
212 (15.8%)
229 (17.1%)
225 (16.8%)
446 (33.3%)		 1338
(91.3%)
polmoral_b To what extent is your political ideology based in your core moral values? 1. [1] 1
2. [2] 2
3. [3] 3
4. [4] 4
5. [5] 5
6. [6] 6
7. [7] 7		 77 ( 5.8%)
34 ( 2.5%)
82 ( 6.1%)
181 (13.5%)
253 (18.9%)
255 (19.1%)
456 (34.1%)		 1338
(91.3%)
polStrength Mean (sd) : 5.2 (1.6)
min < med < max:
1 < 5.5 < 7
IQR (CV) : 2.5 (0.3)		 13 distinct values 1338
(91.3%)
suppoppRep Are your political views motivated more by support for Republicans, or by opposition to Democrats? 1. [1] 1 - not at all
2. [2] 2
3. [3] 3
4. [4] 4
5. [5] 5
6. [6] 6
7. [7] 7 - very much		 141 (22.6%)
69 (11.1%)
66 (10.6%)
233 (37.3%)
42 ( 6.7%)
23 ( 3.7%)
50 ( 8.0%)		 624
(42.6%)
suppoppDem Are your political views motivated more by support for Democrats, or by opposition to Republicans? 1. [1] 1 - not at all
2. [2] 2
3. [3] 3
4. [4] 4
5. [5] 5
6. [6] 6
7. [7] 7 - very much		 161 (23.1%)
94 (13.5%)
81 (11.6%)
211 (30.2%)
73 (10.5%)
29 ( 4.2%)
49 ( 7.0%)		 698
(47.6%)
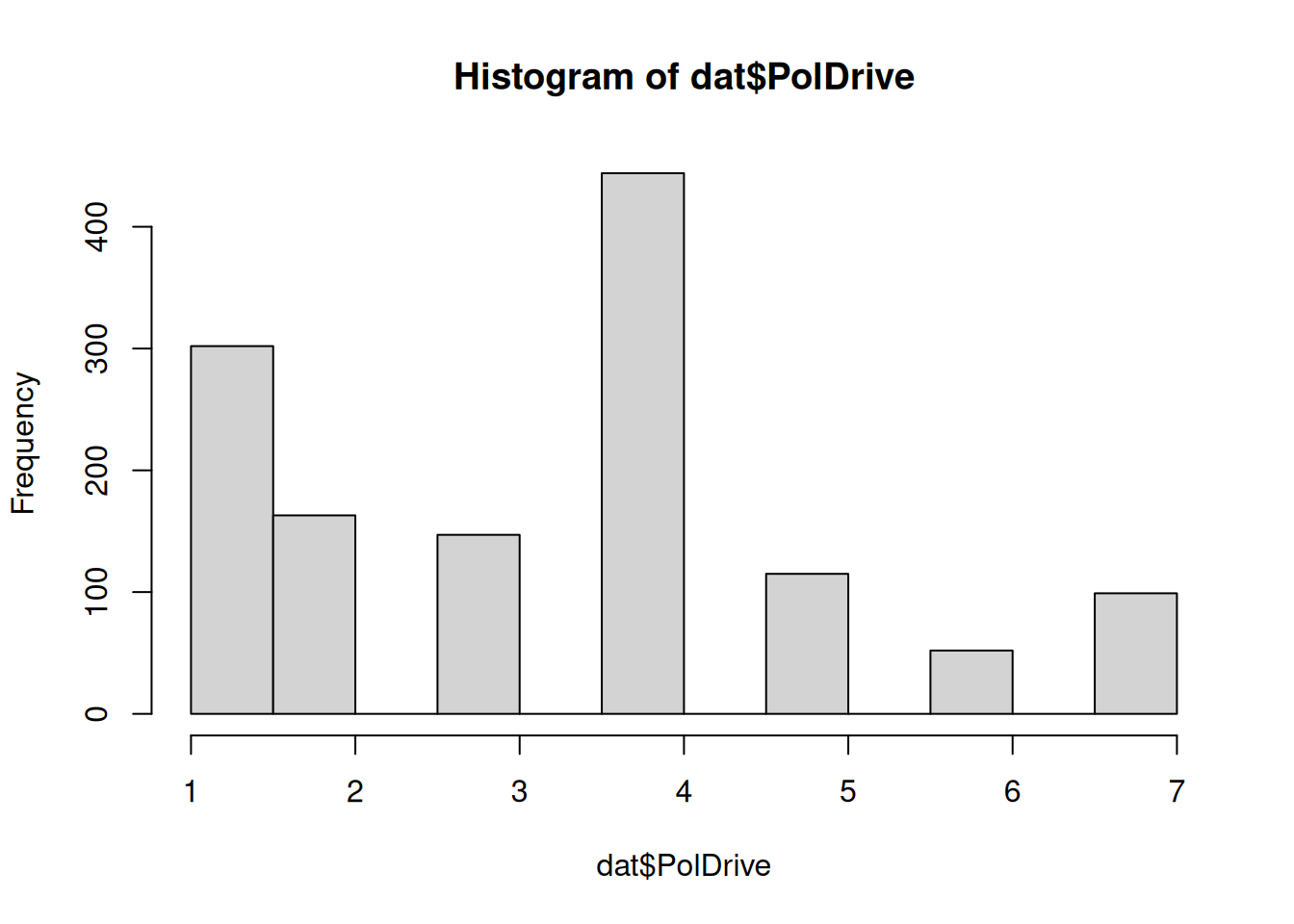
PolDrive Mean (sd) : 3.3 (1.8)
min < med < max:
1 < 4 < 7
IQR (CV) : 2 (0.5)		 1 : 302 (22.8%)
2 : 163 (12.3%)
3 : 147 (11.1%)
4 : 444 (33.6%)
5 : 115 ( 8.7%)
6 : 52 ( 3.9%)
7 : 99 ( 7.5%)		 1322
(90.2%)
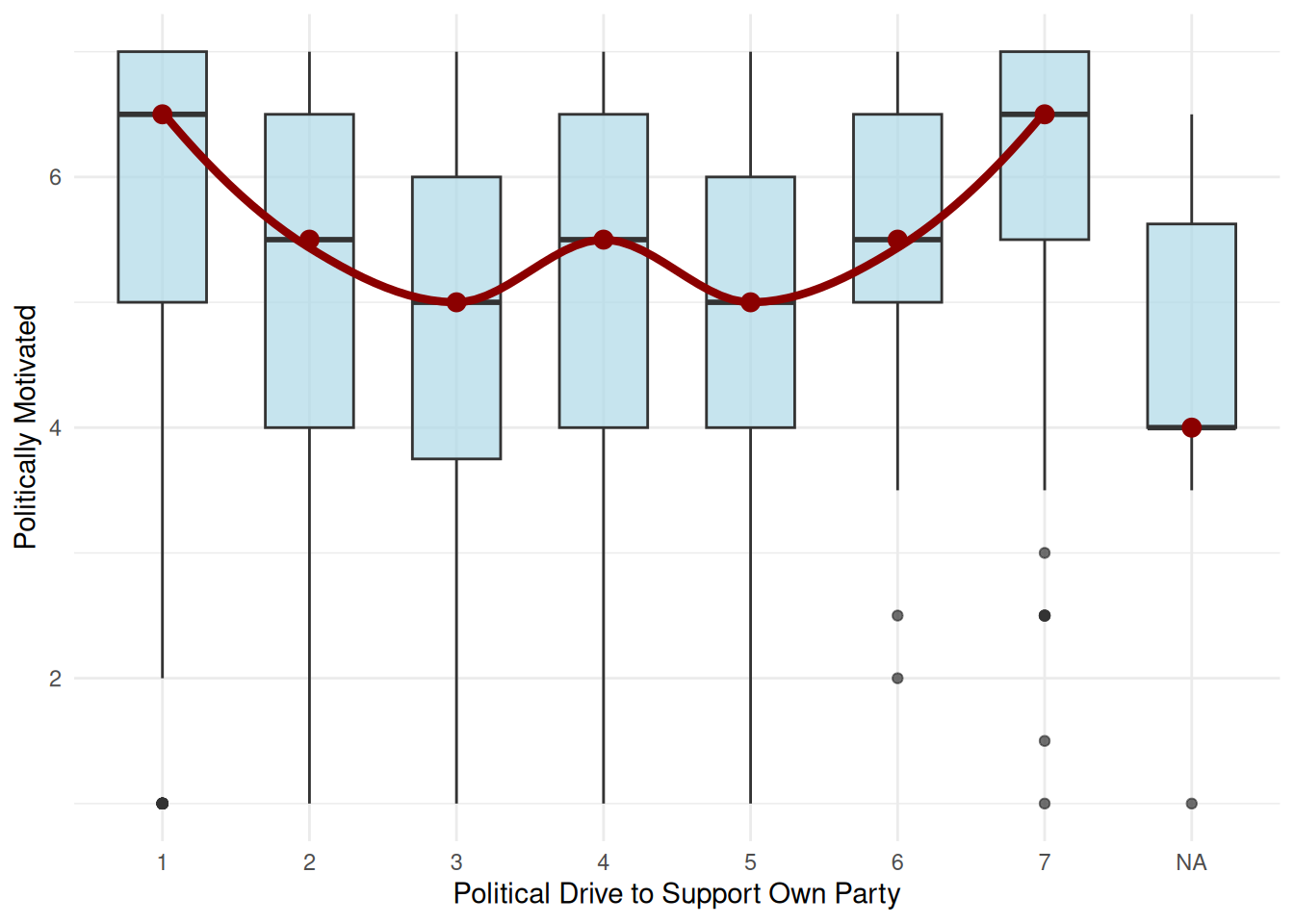
polDrvSupOwnParty Mean (sd) : 3.3 (1.8)
min < med < max:
1 < 4 < 7
IQR (CV) : 2 (0.5)		 1 : 302 (22.8%)
2 : 163 (12.3%)
3 : 147 (11.1%)
4 : 444 (33.6%)
5 : 115 ( 8.7%)
6 : 52 ( 3.9%)
7 : 99 ( 7.5%)		 1322
(90.2%)
SelfInterBene1 In the long term, I appreciate considering a different perspective. 1. [1] 1 - Strongly disagree
2. [2] 2 - Disagree
3. [3] 3 - Somewhat disagree
4. [4] 4 - Neither agree nor
5. [5] 5 - Somewhat agree
6. [6] 6 - Agree
7. [7] 7 - Strongly agree		 56 ( 4.3%)
47 ( 3.6%)
79 ( 6.1%)
368 (28.2%)
332 (25.5%)
241 (18.5%)
181 (13.9%)		 1304
(89.0%)
SIH2 I am willing to change my position on an important issue in the face of good reasons 1. [1] 1 - Strongly Disagree
2. [2] 2
3. [3] 3
4. [4] 4
5. [5] 5
6. [6] 6
7. [7] 7
8. [8] 8
9. [9] 9 - Strongly Agree		 55 ( 4.2%)
27 ( 2.1%)
50 ( 3.8%)
112 ( 8.6%)
191 (14.7%)
172 (13.2%)
230 (17.7%)
194 (14.9%)
268 (20.6%)		 1299
(88.7%)
otherInterBene1 In the long term, other people in my political party appreciate considering a different perspective. 1. [1] 1 - Strongly disagree
2. [2] 2 - Disagree
3. [3] 3 - Somewhat disagree
4. [4] 4 - Neither agree nor
5. [5] 5 - Somewhat agree
6. [6] 6 - Agree
7. [7] 7 - Strongly agree		 46 ( 3.5%)
70 ( 5.4%)
132 (10.1%)
509 (39.0%)
274 (21.0%)
154 (11.8%)
119 ( 9.1%)		 1304
(89.0%)
OtherSIH2 Other people in my political party are willing to change their positions on an important issue in the face of good reasons 1. [1] 1 - Strongly Disagree
2. [2] 2
3. [3] 3
4. [4] 4
5. [5] 5
6. [6] 6
7. [7] 7
8. [8] 8
9. [9] 9 - Strongly Agree		 55 ( 4.2%)
45 ( 3.5%)
68 ( 5.2%)
167 (12.9%)
296 (22.8%)
192 (14.8%)
188 (14.5%)
134 (10.3%)
151 (11.7%)		 1296
(88.5%)
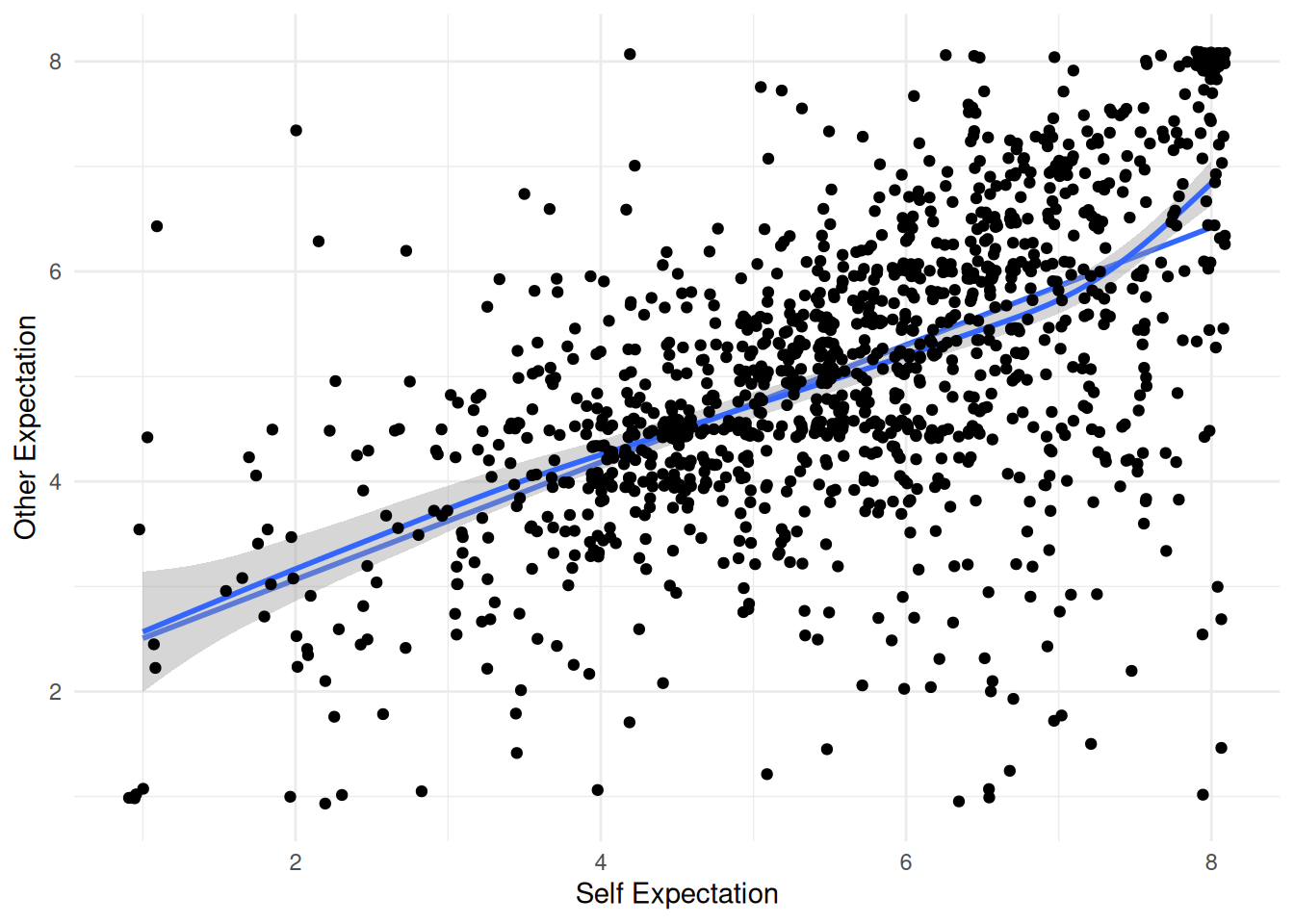
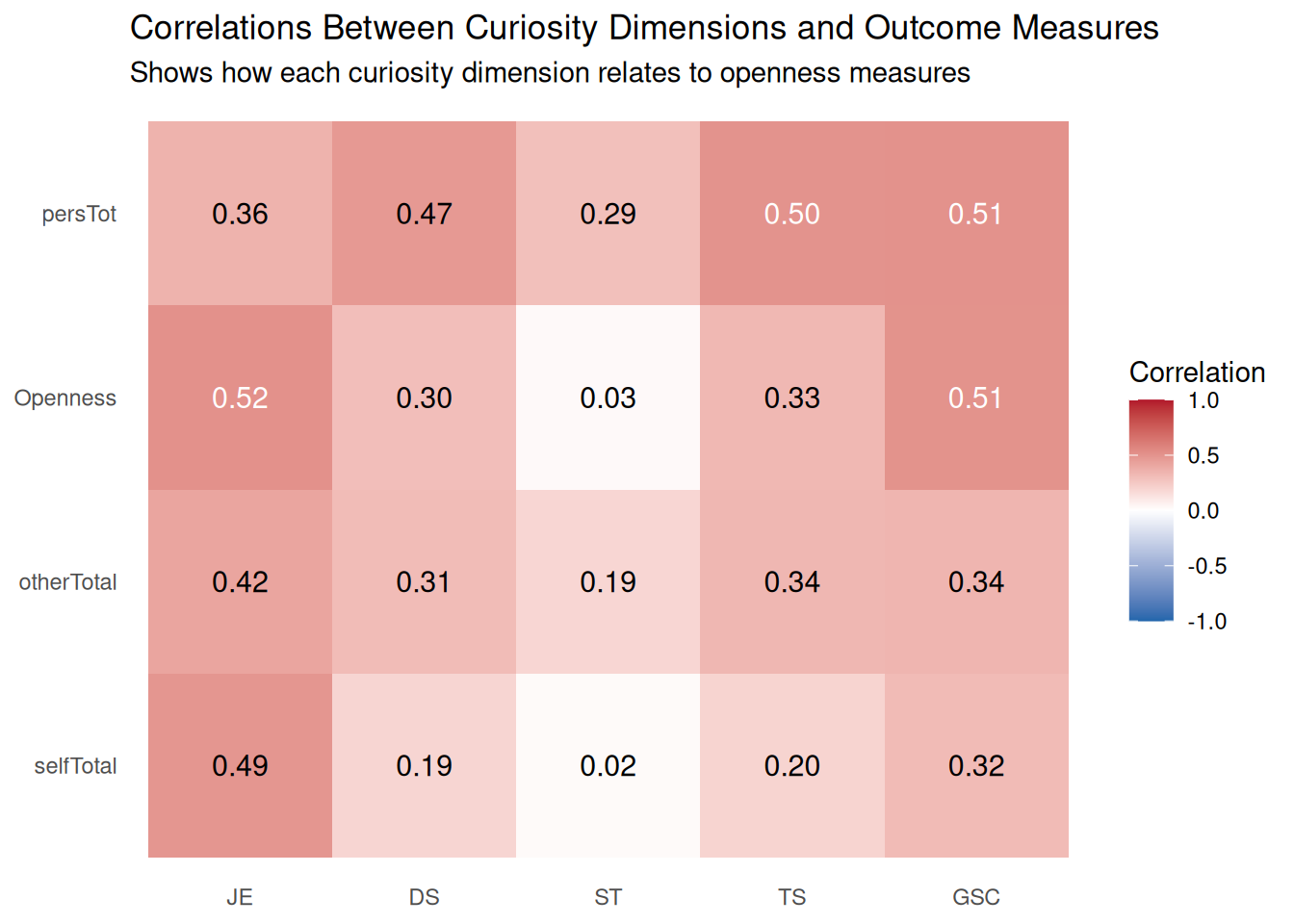
selfTotal Mean (sd) : 5.6 (1.5)
min < med < max:
1 < 5.8 < 8
IQR (CV) : 2.2 (0.3)		 28 distinct values 1299
(88.7%)
otherTotal Mean (sd) : 5.1 (1.4)
min < med < max:
1 < 5 < 8
IQR (CV) : 1.8 (0.3)		 29 distinct values 1296
(88.5%)
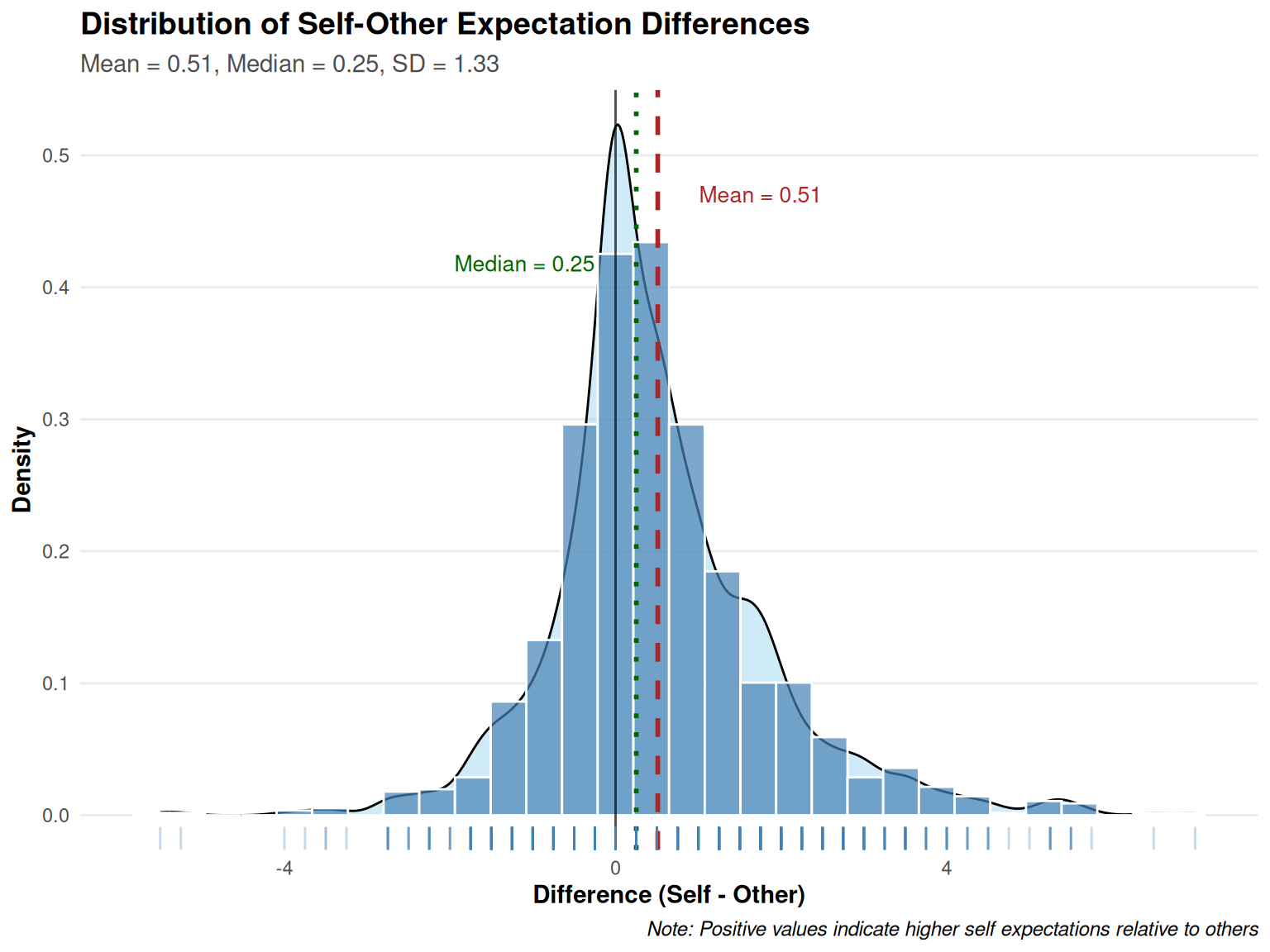
ExpDelta Mean (sd) : 0.5 (1.3)
min < med < max:
-5.5 < 0.2 < 7
IQR (CV) : 1.2 (2.6)		 43 distinct values 1293
(88.3%)
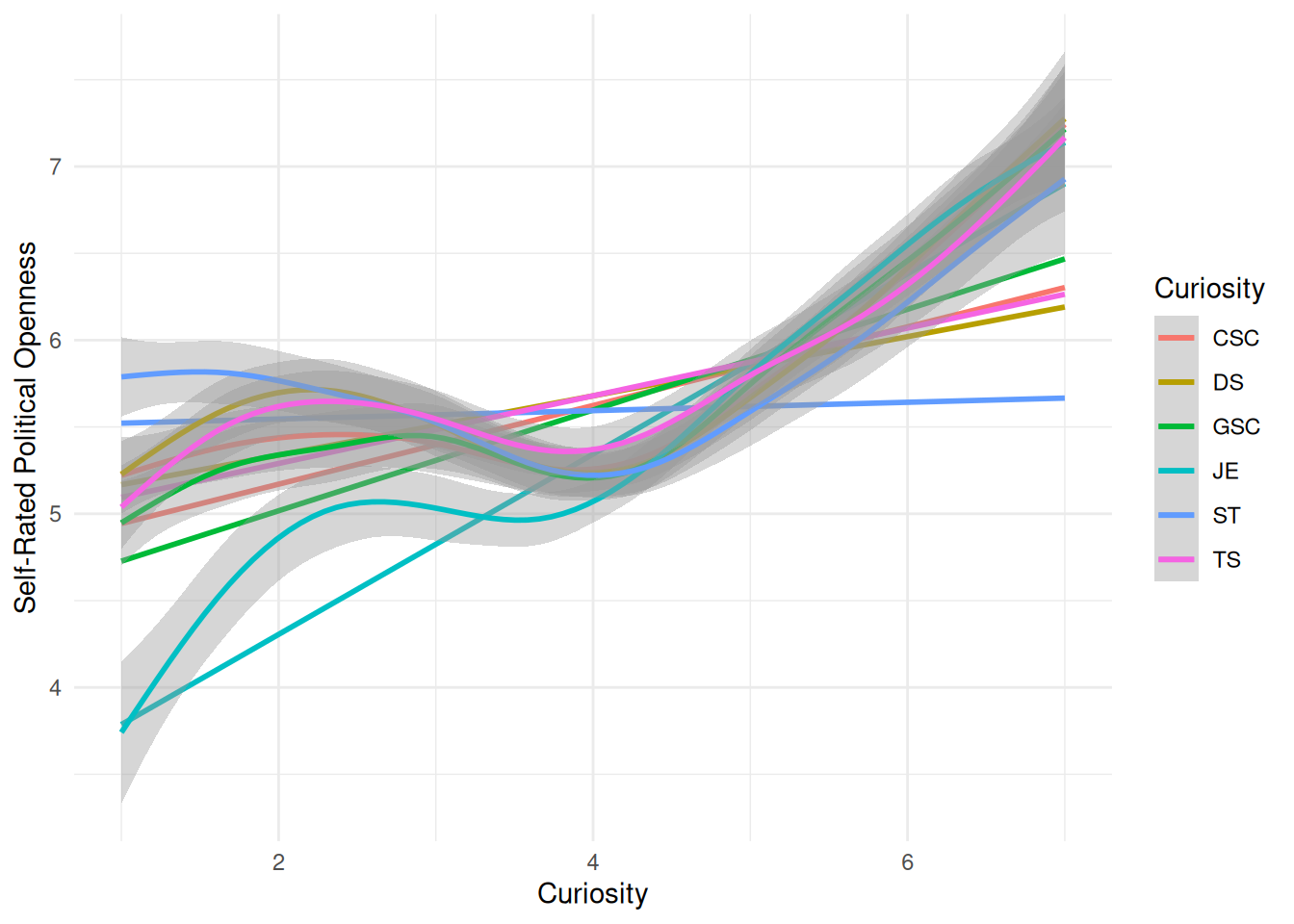
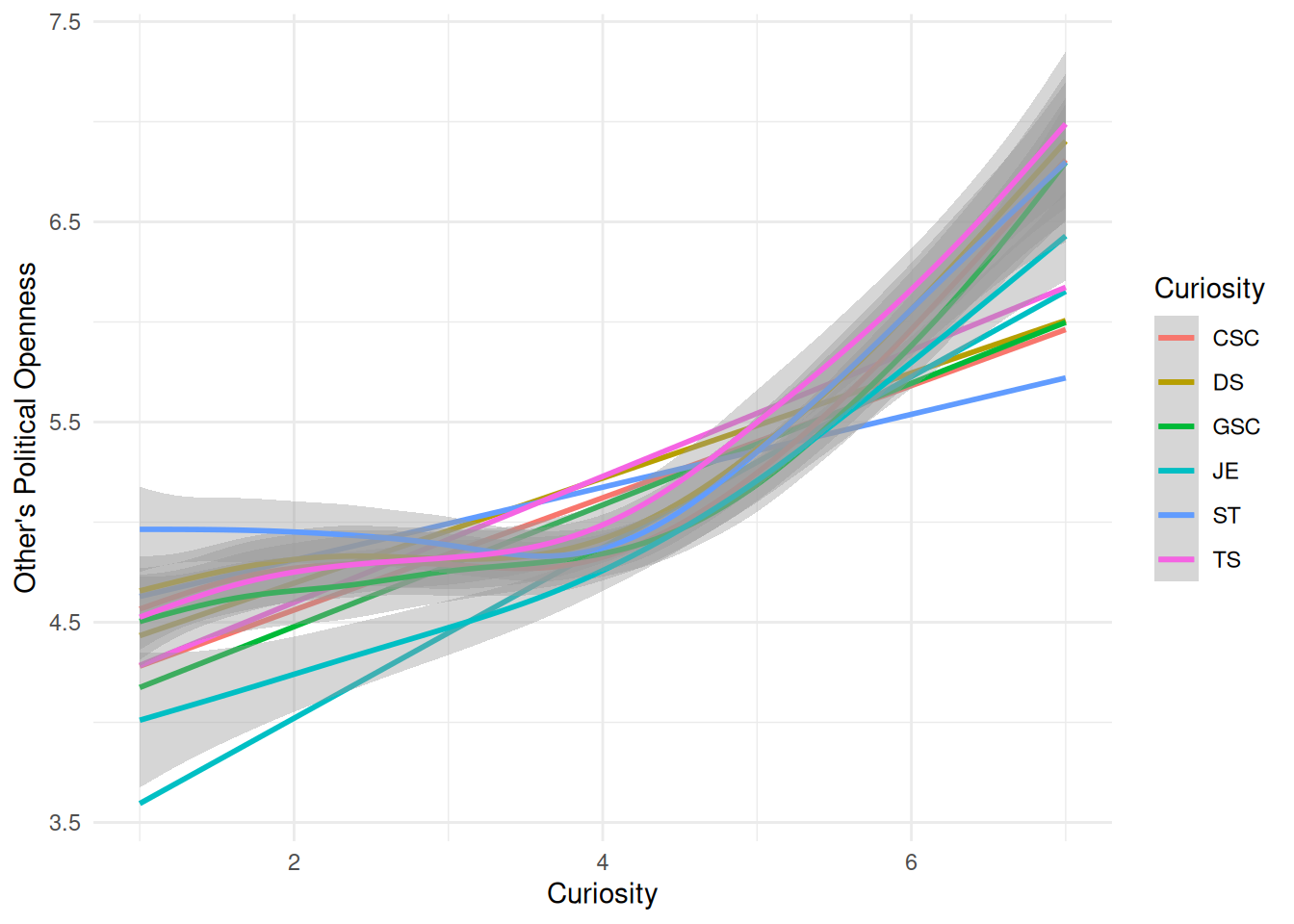
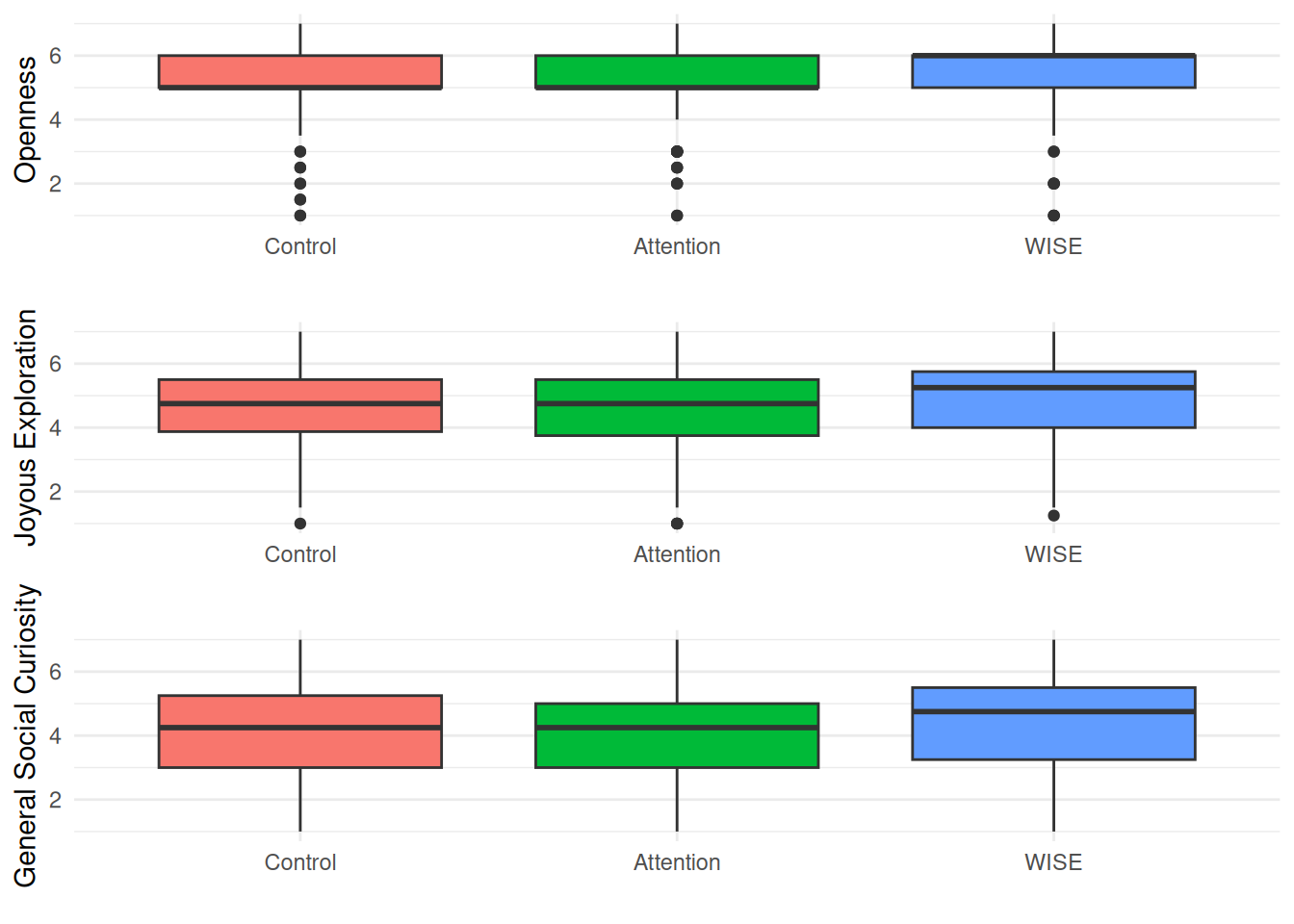
JE Mean (sd) : 4.5 (1.4)
min < med < max:
1 < 4.5 < 7
IQR (CV) : 1.5 (0.3)		 25 distinct values 1242
(84.8%)
DS Mean (sd) : 3.4 (1.7)
min < med < max:
1 < 3.8 < 7
IQR (CV) : 2.5 (0.5)		 25 distinct values 1242
(84.8%)
ST Mean (sd) : 3.4 (1.5)
min < med < max:
1 < 3.5 < 7
IQR (CV) : 2 (0.4)		 25 distinct values 1242
(84.8%)
TS Mean (sd) : 3.5 (1.5)
min < med < max:
1 < 3.8 < 7
IQR (CV) : 2 (0.4)		 25 distinct values 1242
(84.8%)
GSC Mean (sd) : 3.9 (1.6)
min < med < max:
1 < 4 < 7
IQR (CV) : 2 (0.4)		 25 distinct values 1242
(84.8%)
CSC Mean (sd) : 3.8 (1.6)
min < med < max:
1 < 4 < 7
IQR (CV) : 2.5 (0.4)		 25 distinct values 1242
(84.8%)
learn1 When discussing politics, I seek to understand where others are coming from. 1. [1] 1 - Strongly disagree
2. [2] 2 - Disagree
3. [3] 3 - Somewhat disagree
4. [4] 4 - Neither agree nor
5. [5] 5 - Somewhat agree
6. [6] 6 - Agree
7. [7] 7 - Strongly agree		 52 ( 4.2%)
47 ( 3.8%)
66 ( 5.3%)
296 (23.9%)
367 (29.6%)
255 (20.6%)
155 (12.5%)		 1238
(84.5%)
learn2 When discussing politics, I want to learn more about why others believe the things they do. 1. [1] 1 - Strongly disagree
2. [2] 2 - Disagree
3. [3] 3 - Somewhat disagree
4. [4] 4 - Neither agree nor
5. [5] 5 - Somewhat agree
6. [6] 6 - Agree
7. [7] 7 - Strongly agree		 56 ( 4.5%)
51 ( 4.1%)
79 ( 6.4%)
298 (24.1%)
324 (26.2%)
281 (22.7%)
149 (12.0%)		 1238
(84.5%)
Openness Mean (sd) : 4.8 (1.4)
min < med < max:
1 < 5 < 7
IQR (CV) : 2 (0.3)		 13 distinct values 1238
(84.5%)
persuade1 When discussing politics, I seek to convince other people to take my position. 1. [1] 1 - Strongly disagree
2. [2] 2 - Disagree
3. [3] 3 - Somewhat disagree
4. [4] 4 - Neither agree nor
5. [5] 5 - Somewhat agree
6. [6] 6 - Agree
7. [7] 7 - Strongly agree		 165 (13.3%)
149 (12.0%)
134 (10.8%)
370 (29.9%)
220 (17.8%)
117 ( 9.5%)
83 ( 6.7%)		 1238
(84.5%)
persuade2 When discussing politics, I want to show others how correct my opinion is. 1. [1] 1 - Strongly disagree
2. [2] 2 - Disagree
3. [3] 3 - Somewhat disagree
4. [4] 4 - Neither agree nor
5. [5] 5 - Somewhat agree
6. [6] 6 - Agree
7. [7] 7 - Strongly agree		 153 (12.4%)
151 (12.2%)
123 ( 9.9%)
369 (29.8%)
221 (17.9%)
123 ( 9.9%)
98 ( 7.9%)		 1238
(84.5%)
persTot Mean (sd) : 3.9 (1.6)
min < med < max:
1 < 4 < 7
IQR (CV) : 2 (0.4)		 13 distinct values 1238
(84.5%)

Study 2 Variables

Code 
# print out the variable names and labels

dfSummary(dat2_selection[,-1],
          class = F,
          varnumbers = FALSE,
          graph.col = T,
          graph.magnif = 0.85,
          valid.col = T,
          na.col=F,
          tmp.img.dir = "tmp",
          style = "grid",
          plain.ascii = F,
          silent = T)

Data Frame Summary

dat2_selection

Dimensions: 466 x 12
Duplicates: 40

Variable Label Stats / Values Freqs (% of Valid) Graph Valid
Condition 1. (Empty string)
2. Control
3. Intervention		 5 ( 1.1%)
231 (49.6%)
230 (49.4%)		 466
(100.0%)
JE Mean (sd) : 4.2 (1.4)
min < med < max:
1 < 4.5 < 7
IQR (CV) : 2.2 (0.3)		 25 distinct values 423
(90.8%)
DS Mean (sd) : 2.7 (1.2)
min < med < max:
1 < 2.5 < 6.2
IQR (CV) : 1.5 (0.4)		 22 distinct values 423
(90.8%)
ST Mean (sd) : 3 (1.1)
min < med < max:
1 < 3 < 6.2
IQR (CV) : 1.5 (0.4)		 22 distinct values 423
(90.8%)
TS Mean (sd) : 3 (1.3)
min < med < max:
1 < 2.8 < 6.8
IQR (CV) : 2 (0.4)		 24 distinct values 423
(90.8%)
GSC Mean (sd) : 4.1 (1.6)
min < med < max:
1 < 4.2 < 7
IQR (CV) : 2.8 (0.4)		 25 distinct values 423
(90.8%)
learn1 When discussing politics, I seek to understand where others are coming from. 1. [1] 1 - Strongly disagree
2. [2] 2 - Disagree
3. [3] 3 - Somewhat disagree
4. [4] 4 - Neither agree nor
5. [5] 5 - Somewhat agree
6. [6] 6 - Agree
7. [7] 7 - Strongly agree		 4 ( 1.0%)
2 ( 0.5%)
16 ( 3.8%)
25 ( 5.9%)
174 (41.3%)
150 (35.6%)
50 (11.9%)		 421
(90.3%)
learn2 When discussing politics, I want to learn more about why others believe the things they do. 1. [1] 1 - Strongly disagree
2. [2] 2 - Disagree
3. [3] 3 - Somewhat disagree
4. [4] 4 - Neither agree nor
5. [5] 5 - Somewhat agree
6. [6] 6 - Agree
7. [7] 7 - Strongly agree		 3 ( 0.7%)
4 ( 1.0%)
13 ( 3.1%)
21 ( 5.0%)
152 (36.1%)
156 (37.1%)
72 (17.1%)		 421
(90.3%)
Openness Mean (sd) : 5.5 (1)
min < med < max:
1 < 5.5 < 7
IQR (CV) : 1 (0.2)		 12 distinct values 421
(90.3%)
persuade1 When discussing politics, I seek to convince other people to take my position. 1. [1] 1 - Strongly disagree
2. [2] 2 - Disagree
3. [3] 3 - Somewhat disagree
4. [4] 4 - Neither agree nor
5. [5] 5 - Somewhat agree
6. [6] 6 - Agree
7. [7] 7 - Strongly agree		 20 ( 4.8%)
68 (16.2%)
63 (15.0%)
71 (16.9%)
129 (30.6%)
56 (13.3%)
14 ( 3.3%)		 421
(90.3%)
persuade2 When discussing politics, I want to show others how correct my opinion is. 1. [1] 1 - Strongly disagree
2. [2] 2 - Disagree
3. [3] 3 - Somewhat disagree
4. [4] 4 - Neither agree nor
5. [5] 5 - Somewhat agree
6. [6] 6 - Agree
7. [7] 7 - Strongly agree		 26 ( 6.2%)
57 (13.5%)
64 (15.2%)
71 (16.9%)
122 (29.0%)
64 (15.2%)
17 ( 4.0%)		 421
(90.3%)
persTot Mean (sd) : 4.1 (1.5)
min < med < max:
1 < 4.5 < 7
IQR (CV) : 2 (0.4)		 13 distinct values 421
(90.3%)

Study 3 Variables

Code 
dfSummary(dat3_selection[,-1],
          class = F,
          varnumbers = FALSE,
          graph.col = T,
          graph.magnif = 0.85,
          valid.col = T,
          na.col=F,
          tmp.img.dir = "tmp",
          style = "grid",
          plain.ascii = F,
          silent = T)

Data Frame Summary

dat3_selection

Dimensions: 651 x 25
Duplicates: 0

Variable Label Stats / Values Freqs (% of Valid) Graph Valid
Condition Mean (sd) : 1 (0.8)
min < med < max:
0 < 1 < 2
IQR (CV) : 2 (0.8)		 0 : 218 (33.5%)
1 : 216 (33.2%)
2 : 217 (33.3%)		 651
(100.0%)
JE Mean (sd) : 4.5 (1.4)
min < med < max:
1 < 4.8 < 7
IQR (CV) : 1.8 (0.3)		 25 distinct values 647
(99.4%)
DS Mean (sd) : 2.6 (1.5)
min < med < max:
1 < 2.2 < 7
IQR (CV) : 2.5 (0.6)		 25 distinct values 647
(99.4%)
ST Mean (sd) : 2.8 (1.3)
min < med < max:
1 < 2.5 < 7
IQR (CV) : 2 (0.5)		 24 distinct values 647
(99.4%)
TS Mean (sd) : 2.7 (1.3)
min < med < max:
1 < 2.5 < 6.5
IQR (CV) : 1.8 (0.5)		 23 distinct values 647
(99.4%)
GSC Mean (sd) : 3.8 (1.5)
min < med < max:
1 < 4 < 7
IQR (CV) : 2.5 (0.4)		 25 distinct values 647
(99.4%)
JEb Mean (sd) : 4.7 (1.4)
min < med < max:
1 < 5 < 7
IQR (CV) : 1.8 (0.3)		 25 distinct values 590
(90.6%)
DSb Mean (sd) : 2.6 (1.5)
min < med < max:
1 < 2.2 < 7
IQR (CV) : 2.5 (0.6)		 25 distinct values 590
(90.6%)
STb Mean (sd) : 3 (1.3)
min < med < max:
1 < 3 < 7
IQR (CV) : 2 (0.4)		 25 distinct values 590
(90.6%)
TSb Mean (sd) : 2.8 (1.3)
min < med < max:
1 < 2.5 < 6.8
IQR (CV) : 2 (0.5)		 23 distinct values 590
(90.6%)
GSCb Mean (sd) : 4.2 (1.5)
min < med < max:
1 < 4.2 < 7
IQR (CV) : 2.2 (0.4)		 25 distinct values 590
(90.6%)
JE2 Mean (sd) : 4.4 (1.6)
min < med < max:
1 < 5 < 7
IQR (CV) : 3 (0.4)		 1 : 38 ( 5.9%)
2 : 80 (12.4%)
3 : 73 (11.3%)
4 : 86 (13.3%)
5 : 198 (30.6%)
6 : 129 (19.9%)
7 : 43 ( 6.6%)		 647
(99.4%)
GSC2 Mean (sd) : 4.2 (1.8)
min < med < max:
1 < 5 < 7
IQR (CV) : 2 (0.4)		 1 : 72 (11.1%)
2 : 63 ( 9.7%)
3 : 90 (13.9%)
4 : 84 (13.0%)
5 : 188 (29.1%)
6 : 104 (16.1%)
7 : 46 ( 7.1%)		 647
(99.4%)
learn1.x When discussing politics, I seek to understand where others are coming from. 1. [1] 1 - Strongly disagree
2. [2] 2 - Disagree
3. [3] 3 - Somewhat disagree
4. [4] 4 - Neither agree nor
5. [5] 5 - Somewhat agree
6. [6] 6 - Agree
7. [7] 7 - Strongly agree		 13 ( 2.0%)
26 ( 4.0%)
35 ( 5.4%)
70 (10.8%)
227 (35.1%)
207 (32.0%)
69 (10.7%)		 647
(99.4%)
learn2.x When discussing politics, I want to learn more about why others believe the things they do. 1. [1] 1 - Strongly disagree
2. [2] 2 - Disagree
3. [3] 3 - Somewhat disagree
4. [4] 4 - Neither agree nor
5. [5] 5 - Somewhat agree
6. [6] 6 - Agree
7. [7] 7 - Strongly agree		 13 ( 2.0%)
20 ( 3.1%)
30 ( 4.6%)
59 ( 9.1%)
231 (35.7%)
210 (32.5%)
84 (13.0%)		 647
(99.4%)
Openness Mean (sd) : 5.2 (1.2)
min < med < max:
1 < 5 < 7
IQR (CV) : 1 (0.2)		 13 distinct values 647
(99.4%)
persuade1.x When discussing politics, I seek to convince other people to take my position. 1. [1] 1 - Strongly disagree
2. [2] 2 - Disagree
3. [3] 3 - Somewhat disagree
4. [4] 4 - Neither agree nor
5. [5] 5 - Somewhat agree
6. [6] 6 - Agree
7. [7] 7 - Strongly agree		 54 ( 8.3%)
109 (16.8%)
83 (12.8%)
119 (18.4%)
195 (30.1%)
72 (11.1%)
15 ( 2.3%)		 647
(99.4%)
persuade2.x When discussing politics, I want to show others how correct my opinion is. 1. [1] 1 - Strongly disagree
2. [2] 2 - Disagree
3. [3] 3 - Somewhat disagree
4. [4] 4 - Neither agree nor
5. [5] 5 - Somewhat agree
6. [6] 6 - Agree
7. [7] 7 - Strongly agree		 64 ( 9.9%)
107 (16.5%)
69 (10.7%)
122 (18.9%)
182 (28.1%)
79 (12.2%)
24 ( 3.7%)		 647
(99.4%)
persTot Mean (sd) : 3.9 (1.5)
min < med < max:
1 < 4 < 7
IQR (CV) : 2.5 (0.4)		 13 distinct values 647
(99.4%)
learn1.y When discussing politics, I seek to understand where others are coming from. 1. [1] 1 - Strongly disagree
2. [2] 2 - Disagree
3. [3] 3 - Somewhat disagree
4. [4] 4 - Neither agree nor
5. [5] 5 - Somewhat agree
6. [6] 6 - Agree
7. [7] 7 - Strongly agree		 8 ( 1.4%)
15 ( 2.5%)
22 ( 3.7%)
55 ( 9.3%)
215 (36.5%)
196 (33.3%)
78 (13.2%)		 589
(90.5%)
learn2.y When discussing politics, I want to learn more about why others believe the things they do. 1. [1] 1 - Strongly disagree
2. [2] 2 - Disagree
3. [3] 3 - Somewhat disagree
4. [4] 4 - Neither agree nor
5. [5] 5 - Somewhat agree
6. [6] 6 - Agree
7. [7] 7 - Strongly agree		 9 ( 1.5%)
14 ( 2.4%)
25 ( 4.2%)
42 ( 7.1%)
215 (36.5%)
201 (34.1%)
83 (14.1%)		 589
(90.5%)
Openness2 Mean (sd) : 5.3 (1.2)
min < med < max:
1 < 5.5 < 7
IQR (CV) : 1 (0.2)		 13 distinct values 589
(90.5%)
persuade1.y When discussing politics, I seek to convince other people to take my position. 1. [1] 1 - Strongly disagree
2. [2] 2 - Disagree
3. [3] 3 - Somewhat disagree
4. [4] 4 - Neither agree nor
5. [5] 5 - Somewhat agree
6. [6] 6 - Agree
7. [7] 7 - Strongly agree		 43 ( 7.3%)
97 (16.5%)
108 (18.3%)
107 (18.2%)
162 (27.5%)
57 ( 9.7%)
15 ( 2.5%)		 589
(90.5%)
persuade2.y When discussing politics, I want to show others how correct my opinion is. 1. [1] 1 - Strongly disagree
2. [2] 2 - Disagree
3. [3] 3 - Somewhat disagree
4. [4] 4 - Neither agree nor
5. [5] 5 - Somewhat agree
6. [6] 6 - Agree
7. [7] 7 - Strongly agree		 48 ( 8.1%)
96 (16.3%)
102 (17.3%)
104 (17.7%)
146 (24.8%)
74 (12.6%)
19 ( 3.2%)		 589
(90.5%)
persTot2 Mean (sd) : 3.8 (1.5)
min < med < max:
1 < 4 < 7
IQR (CV) : 2.5 (0.4)		 13 distinct values 589
(90.5%)

Missing Data

We conducted extensive missing data analyses on the data and even ran the models using multiple imputation. The results were similar to the results we present in the paper. We decided to use the data as is (aka complete case analysis or listwise deletion) because the missing data was not random later in the study progression. Why? The panel design led to dropouts that were monotonically missing and, by definition, fall into the MAR mechanism of missing data. Here are the missing data plots for the three data sources. When looking at each individual dataset, we found the data to be MCAR but we know that these tests - in isolation - are not useful in determining longitudinal or panel design missing data mechanisms across studies. Thus, the MCAR tests are not useful in this case.

Code 
misscheck <- function(data) {
  tmp <- data %>% 
    gather(key = "key", value = "val") %>%
    mutate(isna = is.na(val)) %>%
    group_by(key) %>%
    mutate(total = n()) %>%
    group_by(key, total, isna) %>%
    summarise(num.isna = n()) %>%
    mutate(pct = num.isna / total * 100)
  
  levels <-
    (tmp  %>% filter(isna == T) %>% arrange(desc(pct)))$key
  
  percentage.plot <- tmp %>%
    ggplot() +
    geom_bar(aes(x = reorder(key, desc(pct)), 
                 y = pct, fill=isna), 
             stat = 'identity', alpha=0.8) +
    scale_x_discrete(limits = levels) +
    scale_fill_manual(name = "", 
                      values = c('black', 'green'), 
                      labels = c("Present", "Missing")) +
    coord_flip() +
    labs(title = paste("Percentage of missing values in", deparse(substitute(data))),          x = 'Variable', 
         y = "% of missing values")
  plot(percentage.plot)
}

misscheck(dat_selection)

Code 
misscheck(dat2_selection)

Code 
misscheck(dat3_selection)

Code 
dat$ATTcheck_pass_fail <- "FAIL"
dat$ATTcheck_pass_fail[dat$attnchck_b == "I know the muffin man"] <- "PASS"

table(dat$ATTcheck_pass_fail)

FAIL PASS 
 593  872

SESSION INFORMATION

Code 
sessioninfo::session_info()
─ Session info ───────────────────────────────────────────────────────────────
 setting  value
 version  R version 4.5.1 (2025-06-13)
 os       Ubuntu 24.04.2 LTS
 system   x86_64, linux-gnu
 ui       X11
 language en_US
 collate  en_US.UTF-8
 ctype    en_US.UTF-8
 tz       America/New_York
 date     2025-07-23
 pandoc   3.4 @ /usr/lib/rstudio/resources/app/bin/quarto/bin/tools/x86_64/ (via rmarkdown)
 quarto   1.6.43 @ /usr/local/bin/quarto

─ Packages ───────────────────────────────────────────────────────────────────
 package       * version    date (UTC) lib source
 aaRon         * 0.1.0      2025-05-10 [1] Github (Aaron0696/aaRon@751c04c)
 abind           1.4-8      2024-09-12 [1] CRAN (R 4.5.0)
 arm             1.14-4     2024-04-01 [1] CRAN (R 4.5.0)
 backports       1.5.0      2024-05-23 [1] CRAN (R 4.5.0)
 base64enc       0.1-3      2015-07-28 [1] CRAN (R 4.5.0)
 bayestestR      0.15.3     2025-04-28 [1] CRAN (R 4.5.0)
 boot            1.3-31     2024-08-28 [4] CRAN (R 4.4.2)
 broom         * 1.0.8      2025-03-28 [1] CRAN (R 4.5.0)
 broom.mixed   * 0.2.9.6    2024-10-15 [1] CRAN (R 4.5.0)
 cachem          1.1.0      2024-05-16 [1] CRAN (R 4.5.0)
 carData         3.0-5      2022-01-06 [1] CRAN (R 4.5.0)
 checkmate       2.3.2      2024-07-29 [1] CRAN (R 4.5.0)
 cli             3.6.5      2025-04-23 [1] CRAN (R 4.5.0)
 cluster         2.1.8.1    2025-03-12 [4] CRAN (R 4.4.3)
 coda            0.19-4.1   2024-01-31 [1] CRAN (R 4.5.0)
 codetools       0.2-20     2024-03-31 [4] CRAN (R 4.4.0)
 colorspace      2.1-1      2024-07-26 [1] CRAN (R 4.5.0)
 corpcor         1.6.10     2021-09-16 [1] CRAN (R 4.5.0)
 curl            6.2.2      2025-03-24 [1] CRAN (R 4.5.0)
 data.table      1.17.0     2025-02-22 [1] CRAN (R 4.5.0)
 datawizard      1.0.2      2025-03-24 [1] CRAN (R 4.5.0)
 devtools      * 2.4.5      2022-10-11 [1] CRAN (R 4.5.0)
 DiagrammeR      1.0.11     2024-02-02 [1] CRAN (R 4.5.0)
 DiagrammeRsvg   0.1        2016-02-04 [1] CRAN (R 4.5.0)
 digest          0.6.37     2024-08-19 [1] CRAN (R 4.5.0)
 dplyr         * 1.1.4      2023-11-17 [1] CRAN (R 4.5.0)
 effectsize      1.0.0      2024-12-10 [1] CRAN (R 4.5.0)
 ellipsis        0.3.2      2021-04-29 [1] CRAN (R 4.5.0)
 emmeans       * 1.11.1     2025-05-04 [1] CRAN (R 4.5.0)
 estimability    1.5.1      2024-05-12 [1] CRAN (R 4.5.0)
 evaluate        1.0.3      2025-01-10 [1] CRAN (R 4.5.0)
 farver          2.1.2      2024-05-13 [1] CRAN (R 4.5.0)
 fastmap         1.2.0      2024-05-15 [1] CRAN (R 4.5.0)
 fdrtool         1.2.18     2024-08-20 [1] CRAN (R 4.5.0)
 forcats       * 1.0.0      2023-01-29 [1] CRAN (R 4.5.0)
 foreign         0.8-90     2025-03-31 [4] CRAN (R 4.4.3)
 Formula         1.2-5      2023-02-24 [1] CRAN (R 4.5.0)
 fs              1.6.6      2025-04-12 [1] CRAN (R 4.5.0)
 furrr           0.3.1      2022-08-15 [1] CRAN (R 4.5.0)
 future          1.40.0     2025-04-10 [1] CRAN (R 4.5.0)
 generics        0.1.4      2025-05-09 [1] CRAN (R 4.5.0)
 ggeffects       2.2.1      2025-03-11 [1] CRAN (R 4.5.0)
 ggplot2       * 3.5.2      2025-04-09 [1] CRAN (R 4.5.0)
 ggthemes      * 5.1.0      2024-02-10 [1] CRAN (R 4.5.0)
 glasso          1.11       2019-10-01 [1] CRAN (R 4.5.0)
 globals         0.17.0     2025-04-16 [1] CRAN (R 4.5.0)
 glue            1.8.0      2024-09-30 [1] CRAN (R 4.5.0)
 gridExtra     * 2.3        2017-09-09 [1] CRAN (R 4.5.0)
 gt            * 1.0.0      2025-04-05 [1] CRAN (R 4.5.0)
 gtable          0.3.6      2024-10-25 [1] CRAN (R 4.5.0)
 gtools          3.9.5      2023-11-20 [1] CRAN (R 4.5.0)
 haven         * 2.5.4      2023-11-30 [1] CRAN (R 4.5.0)
 Hmisc           5.2-3      2025-03-16 [1] CRAN (R 4.5.0)
 hms             1.1.3      2023-03-21 [1] CRAN (R 4.5.0)
 htmlTable       2.4.3      2024-07-21 [1] CRAN (R 4.5.0)
 htmltools       0.5.8.1    2024-04-04 [1] CRAN (R 4.5.0)
 htmlwidgets     1.6.4      2023-12-06 [1] CRAN (R 4.5.0)
 httpuv          1.6.16     2025-04-16 [1] CRAN (R 4.5.0)
 igraph          2.1.4      2025-01-23 [1] CRAN (R 4.5.0)
 insight         1.2.0      2025-04-22 [1] CRAN (R 4.5.0)
 jpeg            0.1-11     2025-03-21 [1] CRAN (R 4.5.0)
 jsonlite        2.0.0      2025-03-27 [1] CRAN (R 4.5.0)
 kableExtra    * 1.4.0      2024-01-24 [1] CRAN (R 4.5.0)
 knitr         * 1.50       2025-03-16 [1] CRAN (R 4.5.0)
 kutils          1.73       2023-09-17 [1] CRAN (R 4.5.0)
 labeling        0.4.3      2023-08-29 [1] CRAN (R 4.5.0)
 later           1.4.2      2025-04-08 [1] CRAN (R 4.5.0)
 lattice         0.22-5     2023-10-24 [4] CRAN (R 4.3.3)
 lavaan        * 0.6-19     2024-09-26 [1] CRAN (R 4.5.0)
 lavaanPlot    * 0.8.1      2024-01-29 [1] CRAN (R 4.5.0)
 lifecycle       1.0.4      2023-11-07 [1] CRAN (R 4.5.0)
 lisrelToR       0.3        2024-02-07 [1] CRAN (R 4.5.0)
 listenv         0.9.1      2024-01-29 [1] CRAN (R 4.5.0)
 lme4          * 1.1-37     2025-03-26 [1] CRAN (R 4.5.0)
 lmerTest      * 3.1-3      2020-10-23 [1] CRAN (R 4.5.0)
 lubridate       1.9.4      2024-12-08 [1] CRAN (R 4.5.0)
 magick          2.8.6      2025-03-23 [1] CRAN (R 4.5.0)
 magrittr        2.0.3      2022-03-30 [1] CRAN (R 4.5.0)
 MASS            7.3-65     2025-02-28 [4] CRAN (R 4.4.3)
 Matrix        * 1.7-3      2025-03-11 [4] CRAN (R 4.4.3)
 matrixStats     1.5.0      2025-01-07 [1] CRAN (R 4.5.0)
 memoise         2.0.1      2021-11-26 [1] CRAN (R 4.5.0)
 mgcv            1.9-1      2023-12-21 [4] CRAN (R 4.3.2)
 mi              1.1        2022-06-06 [1] CRAN (R 4.5.0)
 mime            0.13       2025-03-17 [1] CRAN (R 4.5.0)
 miniUI          0.1.2      2025-04-17 [1] CRAN (R 4.5.0)
 minqa           1.2.8      2024-08-17 [1] CRAN (R 4.5.0)
 mnormt          2.1.1      2022-09-26 [1] CRAN (R 4.5.0)
 modelsummary  * 2.3.0      2025-02-02 [1] CRAN (R 4.5.0)
 mvtnorm         1.3-3      2025-01-10 [1] CRAN (R 4.5.0)
 nlme            3.1-168    2025-03-31 [4] CRAN (R 4.4.3)
 nloptr          2.2.1      2025-03-17 [1] CRAN (R 4.5.0)
 nnet            7.3-20     2025-01-01 [4] CRAN (R 4.4.2)
 numDeriv        2016.8-1.1 2019-06-06 [1] CRAN (R 4.5.0)
 OpenMx          2.21.13    2024-10-19 [1] CRAN (R 4.5.0)
 openxlsx        4.2.8      2025-01-25 [1] CRAN (R 4.5.0)
 pander          0.6.6      2025-03-01 [1] CRAN (R 4.5.0)
 parallelly      1.43.0     2025-03-24 [1] CRAN (R 4.5.0)
 parameters      0.25.0     2025-04-30 [1] CRAN (R 4.5.0)
 pbapply         1.7-2      2023-06-27 [1] CRAN (R 4.5.0)
 pbivnorm        0.6.0      2015-01-23 [1] CRAN (R 4.5.0)
 performance     0.13.0     2025-01-15 [1] CRAN (R 4.5.0)
 pillar          1.10.2     2025-04-05 [1] CRAN (R 4.5.0)
 pkgbuild        1.4.7      2025-03-24 [1] CRAN (R 4.5.0)
 pkgconfig       2.0.3      2019-09-22 [1] CRAN (R 4.5.0)
 pkgload         1.4.0      2024-06-28 [1] CRAN (R 4.5.0)
 plyr            1.8.9      2023-10-02 [1] CRAN (R 4.5.0)
 png             0.1-8      2022-11-29 [1] CRAN (R 4.5.0)
 profvis         0.4.0      2024-09-20 [1] CRAN (R 4.5.0)
 promises        1.3.2      2024-11-28 [1] CRAN (R 4.5.0)
 pryr            0.1.6      2023-01-17 [1] CRAN (R 4.5.0)
 psych         * 2.5.3      2025-03-21 [1] CRAN (R 4.5.0)
 purrr           1.0.4      2025-02-05 [1] CRAN (R 4.5.0)
 qgraph          1.9.8      2023-11-03 [1] CRAN (R 4.5.0)
 quadprog        1.5-8      2019-11-20 [1] CRAN (R 4.5.0)
 R6              2.6.1      2025-02-15 [1] CRAN (R 4.5.0)
 ragg            1.4.0      2025-04-10 [1] CRAN (R 4.5.0)
 rapportools     1.2        2025-02-28 [1] CRAN (R 4.5.0)
 rbibutils       2.3        2024-10-04 [1] CRAN (R 4.5.0)
 RColorBrewer    1.1-3      2022-04-03 [1] CRAN (R 4.5.0)
 Rcpp            1.0.14     2025-01-12 [1] CRAN (R 4.5.0)
 RcppParallel    5.1.10     2025-01-24 [1] CRAN (R 4.5.0)
 Rdpack          2.6.4      2025-04-09 [1] CRAN (R 4.5.0)
 readr           2.1.5      2024-01-10 [1] CRAN (R 4.5.0)
 reformulas      0.4.1      2025-04-30 [1] CRAN (R 4.5.0)
 remotes         2.5.0      2024-03-17 [1] CRAN (R 4.5.0)
 reshape2      * 1.4.4      2020-04-09 [1] CRAN (R 4.5.0)
 rlang           1.1.6      2025-04-11 [1] CRAN (R 4.5.0)
 rmarkdown       2.29       2024-11-04 [1] CRAN (R 4.5.0)
 rockchalk       1.8.157    2022-08-06 [1] CRAN (R 4.5.0)
 rpart           4.1.24     2025-01-07 [4] CRAN (R 4.4.2)
 rstudioapi      0.17.1     2024-10-22 [1] CRAN (R 4.5.0)
 rsvg            2.6.2      2025-03-23 [1] CRAN (R 4.5.0)
 scales          1.4.0      2025-04-24 [1] CRAN (R 4.5.0)
 sem             3.1-16     2024-08-28 [1] CRAN (R 4.5.0)
 semPlot       * 1.1.6      2022-08-10 [1] CRAN (R 4.5.0)
 semTools      * 0.5-7      2025-03-13 [1] CRAN (R 4.5.0)
 sessioninfo     1.2.3      2025-02-05 [1] CRAN (R 4.5.0)
 shiny           1.10.0     2024-12-14 [1] CRAN (R 4.5.0)
 sjlabelled    * 1.2.0      2022-04-10 [1] CRAN (R 4.5.0)
 sjmisc          2.8.10     2024-05-13 [1] CRAN (R 4.5.0)
 sjPlot        * 2.8.17     2024-11-29 [1] CRAN (R 4.5.0)
 sjstats         0.19.0     2024-05-14 [1] CRAN (R 4.5.0)
 stringi         1.8.7      2025-03-27 [1] CRAN (R 4.5.0)
 stringr         1.5.1      2023-11-14 [1] CRAN (R 4.5.0)
 summarytools  * 1.1.4      2025-04-29 [1] CRAN (R 4.5.0)
 svglite         2.1.3      2023-12-08 [1] CRAN (R 4.5.0)
 systemfonts     1.2.3      2025-04-30 [1] CRAN (R 4.5.0)
 tables          0.9.31     2024-08-29 [1] CRAN (R 4.5.0)
 textshaping     1.0.1      2025-05-01 [1] CRAN (R 4.5.0)
 tibble          3.2.1      2023-03-20 [1] CRAN (R 4.5.0)
 tidyr         * 1.3.1      2024-01-24 [1] CRAN (R 4.5.0)
 tidyselect      1.2.1      2024-03-11 [1] CRAN (R 4.5.0)
 timechange      0.3.0      2024-01-18 [1] CRAN (R 4.5.0)
 tzdb            0.5.0      2025-03-15 [1] CRAN (R 4.5.0)
 urlchecker      1.0.1      2021-11-30 [1] CRAN (R 4.5.0)
 usethis       * 3.1.0      2024-11-26 [1] CRAN (R 4.5.0)
 V8              6.0.3      2025-03-26 [1] CRAN (R 4.5.0)
 vctrs           0.6.5      2023-12-01 [1] CRAN (R 4.5.0)
 viridis       * 0.6.5      2024-01-29 [1] CRAN (R 4.5.0)
 viridisLite   * 0.4.2      2023-05-02 [1] CRAN (R 4.5.0)
 visNetwork      2.1.2      2022-09-29 [1] CRAN (R 4.5.0)
 withr           3.0.2      2024-10-28 [1] CRAN (R 4.5.0)
 xfun            0.52       2025-04-02 [1] CRAN (R 4.5.0)
 XML             3.99-0.18  2025-01-01 [1] CRAN (R 4.5.0)
 xml2            1.3.8      2025-03-14 [1] CRAN (R 4.5.0)
 xtable          1.8-4      2019-04-21 [1] CRAN (R 4.5.0)
 yaml            2.3.10     2024-07-26 [1] CRAN (R 4.5.0)
 zip             2.3.2      2025-02-01 [1] CRAN (R 4.5.0)

 [1] /home/pem725/R/x86_64-pc-linux-gnu-library/4.5
 [2] /usr/local/lib/R/site-library
 [3] /usr/lib/R/site-library
 [4] /usr/lib/R/library
 * ── Packages attached to the search path.

──────────────────────────────────────────────────────────────────────────────